Предмет: Алгебра,
автор: 444111149
помогите алгебра 2.1
Приложения:
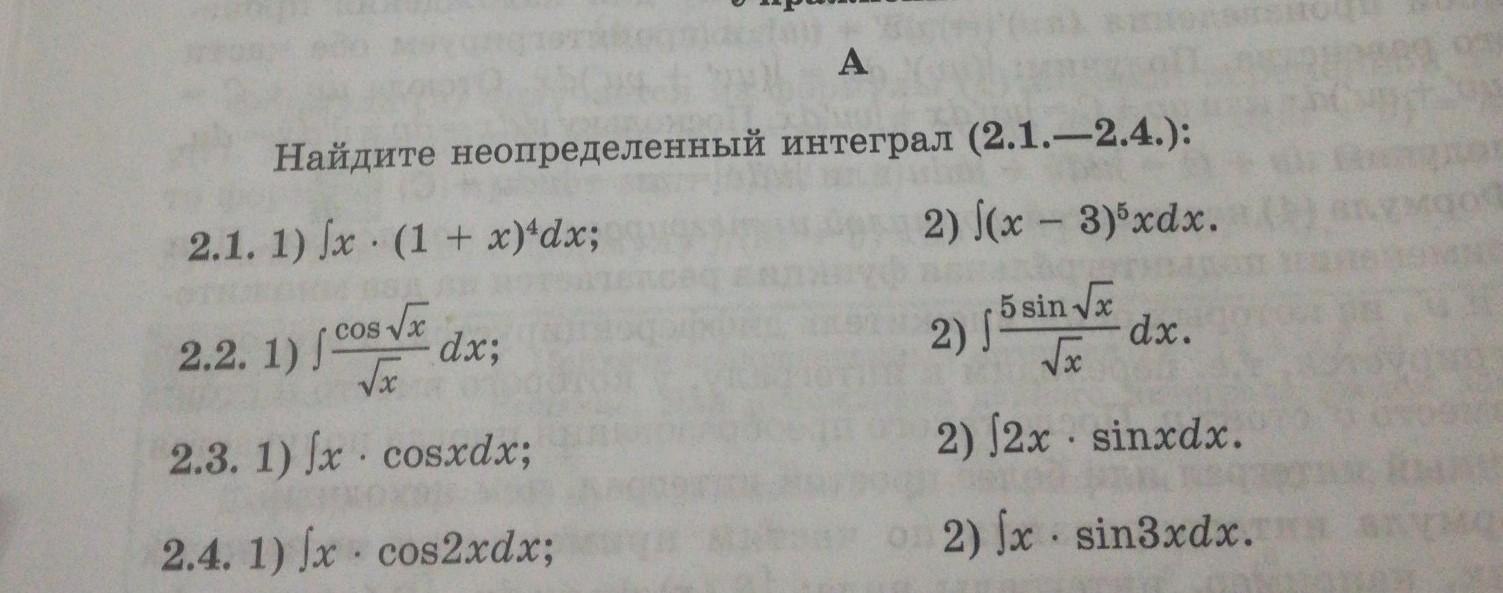
NNNLLL54:
много заданий для одного вопроса ( тем более последние четыре примера на интегрирование по частям - один и тот же метод)
Ответы
Автор ответа:
0
Ответ:
см
Похожие вопросы
Предмет: Русский язык,
автор: Луняев
Предмет: Окружающий мир,
автор: Yanaaaa11
Предмет: Українська мова,
автор: сергг
Предмет: Русский язык,
автор: iraews
Предмет: Русский язык,
автор: Спири1345