Question

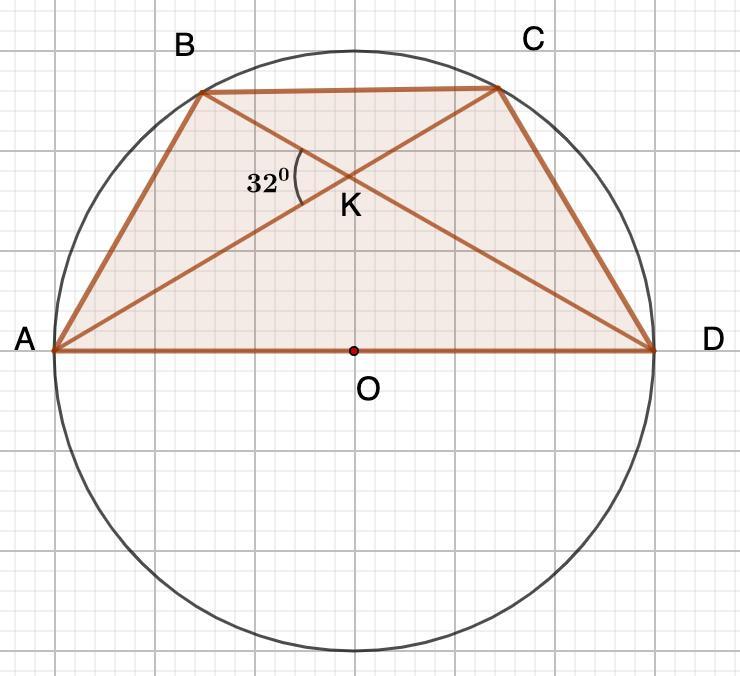
Рівнобічна трапеція вписана в коло, центр якого лежить на більшій основі. Кут між діагоналями трапеції, протилежний її бічній стороні, дорівнює 32°. Знайдіть кути трапеції ​

Answer 1

Ответ:

∠A=∠D=74°

∠B=∠C=106°

Объяснение:

Дано: Окр.О

ABCD -  вписанная трапеция.

∠АКВ=32°

О∈AD

Найти: углы трапеции.

Решение:

1) ABCD - равнобедренная трапеция (вписанная)

∠АКВ=(∪AB+∪CD):2 (угол между пересекающимися хордами)

∪AB=∪CD (равными хордами стягиваются равные дуги)

32°=(∪AB+∪CD):2

2∪АВ=64° ⇒ ∪АВ=∪CD=32°

2) ∠ABD=90° (вписанный, опирается на диаметр)

∠DBC=∪CD:2=32°:2=16° (вписанный)

⇒∠B=∠ABD+∠DBC=90°+16°=106°

3) ∠A=180°-∠B=180°-106°=74° (внутренние односторонние при BC║AD и секущей АВ)

4) Углы при основаниях равнобедренной трапеции равны.

∠A=∠D=74°

∠B=∠C=106°