Предмет: Геометрия,
автор: Anonim00845
На боковой стороне AB равнобедренного треугольника АВС выбрана точка Е, а на продолжении основания АС за точку А выбрана точка D так что [ (угол)BDC = (угол)ЕСА ]. Докажите что площади треугольников DEC = ABC.
P.s. желательно решение по действиям
( 1.
2.
3. ... )
15баллов
Приложения:

Ответы
Автор ответа:
6
Объяснение:
Дано: ΔАВС - равнобедренный.
∠BDC=∠ECA
Доказать:
S (ΔDEC) = S (ΔABC)
Доказательство:
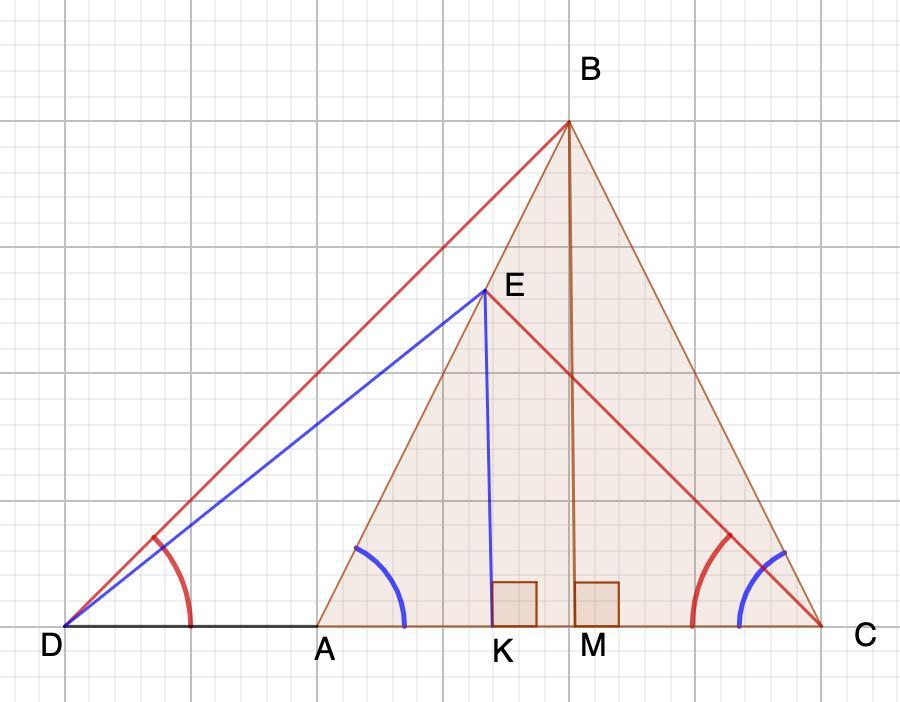
Дополнительное построение: BM⊥DC; EK⊥DC
Если два угла одного треугольника равны двум углам другого треугольника, то эти треугольники подобны.
1) Рассмотрим ΔDBC и ΔАЕС.
∠BDC=∠ECA (условие)
∠ВАС = ∠ВСА (ΔАВС - равнобедренный)
⇒ ΔDBC ~ ΔАЕС
2) ΔDBC ~ ΔАЕС
Составим пропорцию:
По основному свойству пропорции:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: KseniyaMakarova
Предмет: Русский язык,
автор: milawka211
Предмет: Английский язык,
автор: nnn25
Предмет: Математика,
автор: kakdjndd