Предмет: Алгебра,
автор: udalov1719
Исследовать функцию y=4x^4-6x^3 и построить график функции (с подробным решением пожалуйста)
СРОЧНО!
udalov1719:
пожалуйста :(
Ответы
Автор ответа:
0
Объяснение:
1) ОДЗ: х∈R
2) Четность, нечетность:
⇒ функция не является четной или нечетной, то есть общего вида.
3) Нули функции (значения аргумента при которых функция равна нулю):
4) Функция непрерывна, асимптот нет.
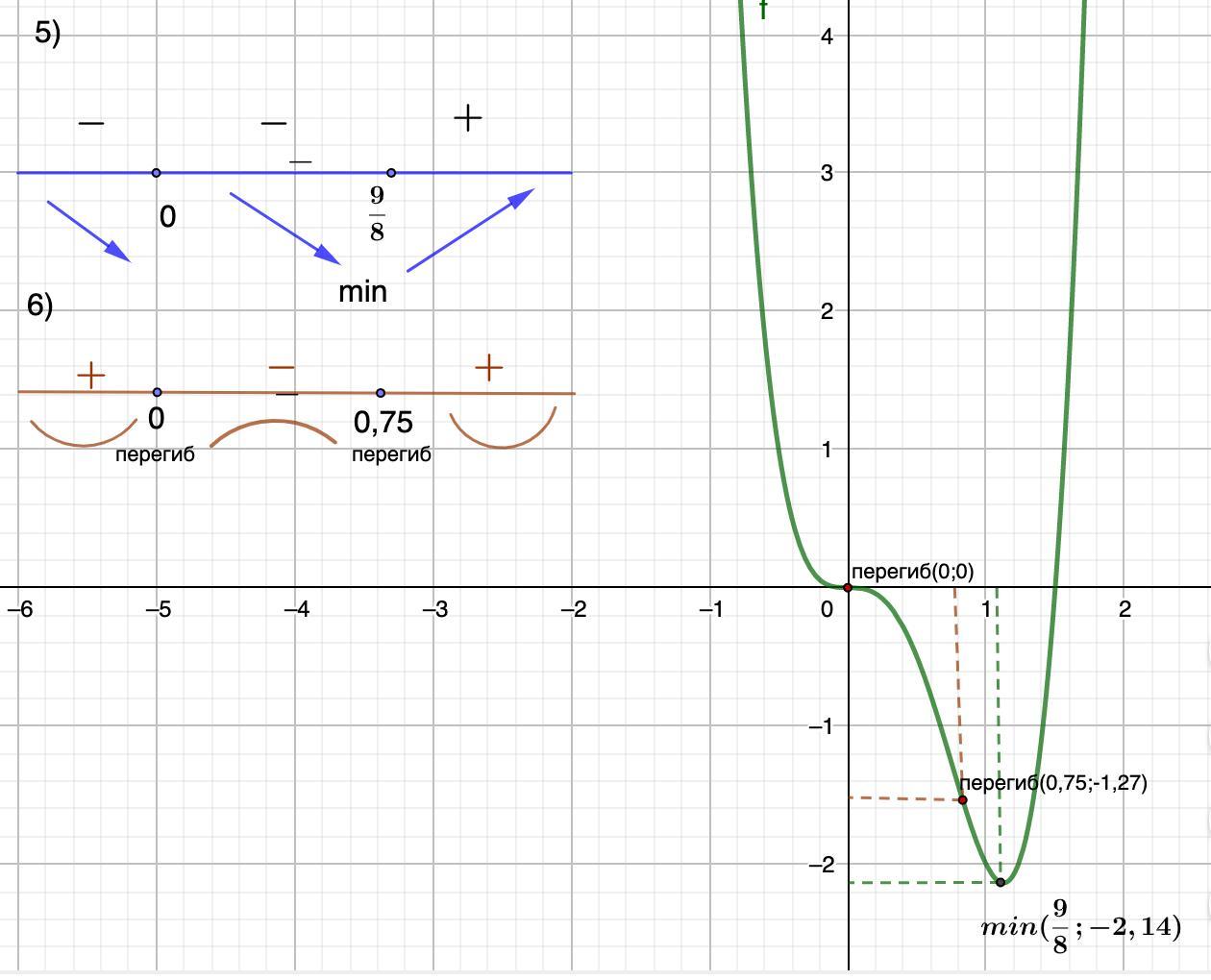
5) Возрастание, убывание:
Найдем производную, приравняем ее к нулю, найдем корни и отметим их на числовой оси. Определим знаки производной на промежутках. Если положительна - функция возрастает, отрицательна - убывает.
(см.рис)
Функция убывает при х∈(-∞; 9/8], возрастает при х∈[9/8; +∞)
6) Выпуклость, вогнутость:
Найдем вторую производную, приравняем ее к нулю, найдем корни и отметим их на числовой оси. Определим знаки второй производной на промежутках. Если положительна - функция вогнута, отрицательна - выпукла.
(см. рис)
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: алина1639
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: nastyaozernova
Предмет: Математика,
автор: GODMODON
Предмет: Английский язык,
автор: almazgame99