Предмет: Алгебра,
автор: Аноним
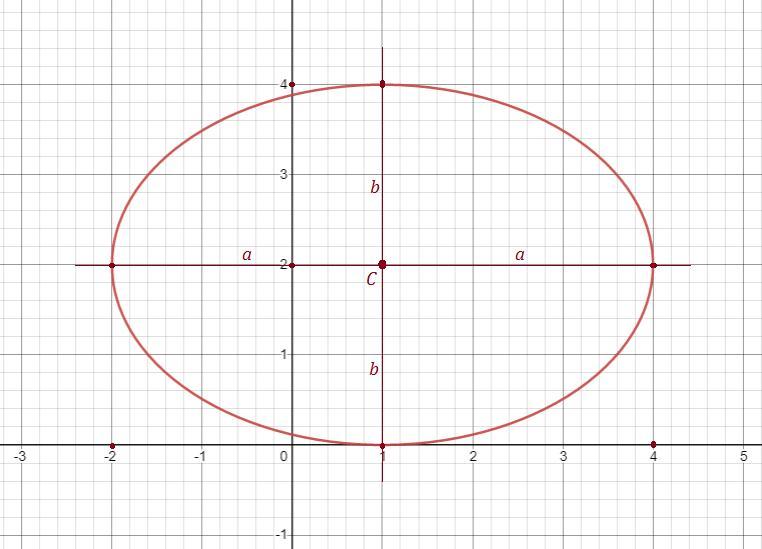
Используя преобразование координат, построить кривую. Указать
координаты центра в новой системе координат, а также полуоси кривой.
Приложения:
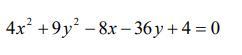
Ответы
Автор ответа:
1
Ответ:
Приложения:
Аноним:
помоги тут, пожалуйста!)
https://znanija.com/task/45371815
можешь тут помочь?
https://znanija.com/task/45486222?answeringSource=feedPublic%2FhomePage%2F1
https://znanija.com/task/45486222?answeringSource=feedPublic%2FhomePage%2F1
Похожие вопросы
Предмет: Окружающий мир,
автор: olgakulakova8
Предмет: Русский язык,
автор: teuxa
Предмет: Русский язык,
автор: ммм125
Предмет: Математика,
автор: TaylerNyashka