Question

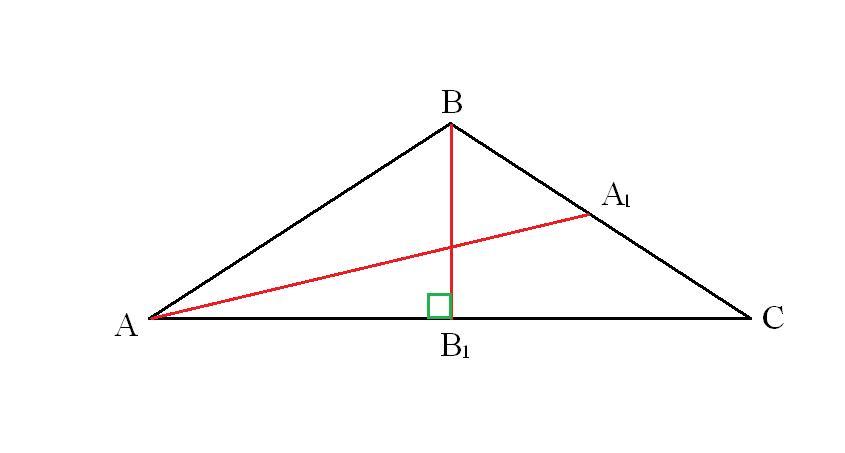
в треугольнике abc в котором угол a = 36 и угол b = 108, проведены биссектрисы aa1 и bb1. докажите что aa1 = 2bb1.​

Answer 1

Ответ:

Пошаговое объяснение:

∠C=180°-(∠A+∠B)=180°-(108°+36°)=36°=∠A⇒∠C=∠A

∠C=∠A⇒ΔABC-равнобедренный⇒BB₁⊥AC

∠BAA₁=∠CAA₁=0,5∠A=0,5·36°=18°

Из ΔABB₁

BB₁=AB·sin∠A=ABsin36°

Из ΔABA₁

∠AA₁B=180°-(∠B+∠BAA₁)=180°-(108°+18°)=54°

AA₁/sin∠B=AB/sin∠AA₁B

AA₁=AB·sin∠B/sin∠AA₁B=AB·sin108°/sin54°=AB·2sin54°·cos54°/sin54°=

=2AB·cos54°=2AB·cos(90°-36°)=2ABsin36°=2BB₁

ч.т.д.