Предмет: Алгебра,
автор: a1d4
lim x-0
tgx-sinx/x^3
ответ 1/2
помогите,пожалуйста
Приложения:
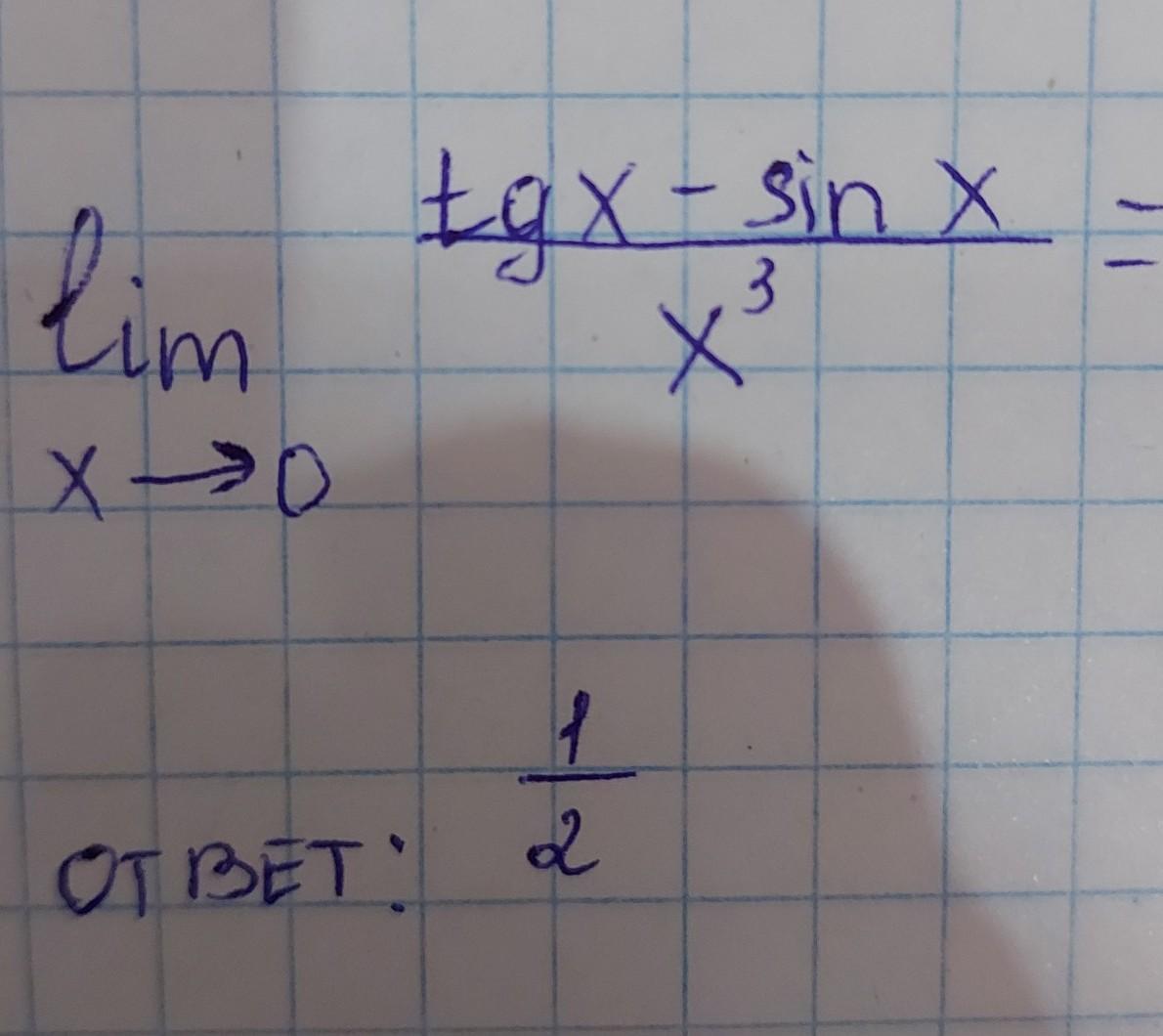
Ответы
Автор ответа:
0
Ответ:
selfcare39:
здравствуйте, помогите пожалуйста с алгеброй, задание у меня в профиле! отмечу 5 звёзд и сделаю лучший ответ!
Похожие вопросы
Предмет: Русский язык,
автор: сынок13
Предмет: Окружающий мир,
автор: Самусенко2005
Предмет: Русский язык,
автор: ZhasaKari
Предмет: Английский язык,
автор: Аноним
Предмет: Химия,
автор: pokerman9019