Предмет: Алгебра,
автор: 5serj2007
Нужно решить двумя способами
1)сложение
2)подставление
Приложения:
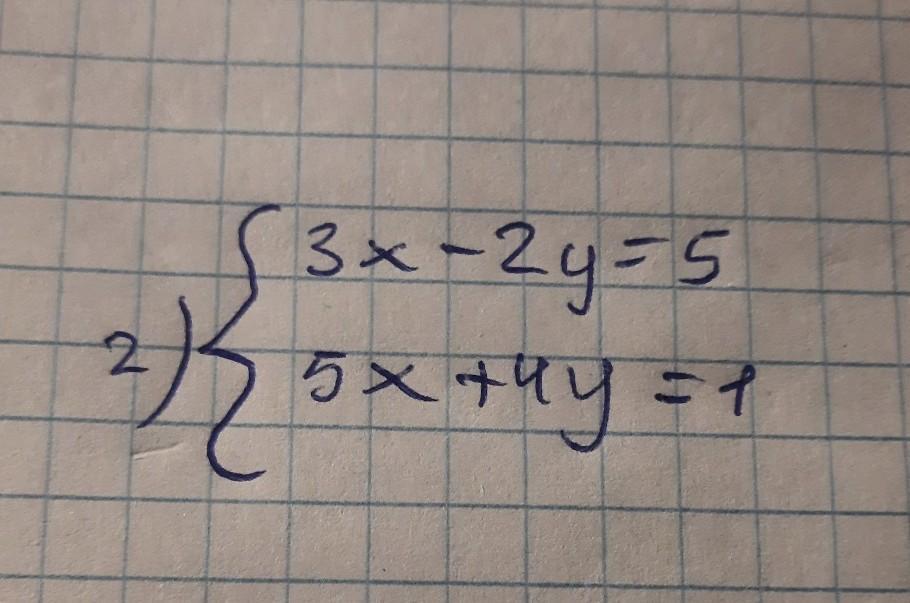
Ответы
Автор ответа:
1
Объяснение:
Метод подстановки:
Метод сложения:
Автор ответа:
1
Ответ:
1) решим методом сложения:
+
Ответ: (1; -1)
2) решим методом подстановки:
Ответ: (1; -1)
Объяснение:
5serj2007:
спасибо большое!
Похожие вопросы
Предмет: Окружающий мир,
автор: vikukulya
Предмет: Русский язык,
автор: Dota2Rulit
Предмет: Английский язык,
автор: али128
Предмет: Русский язык,
автор: pancysik1