Предмет: Геометрия,
автор: mullseven
СРОЧНО! Диагональ осевого сечения цилиндра равна 6 см и составляет с образующей угол 60°. Найдите площадь полной поверхности цилиндра. (С РИСУНКОМ)
Аноним:
R=1,5. Н=3√3; Sпол=2*π*1,5²+2π*1,5*3√3=4,5π+9π√3
Ответы
Автор ответа:
10
Объяснение:
Дано: Цилиндр;
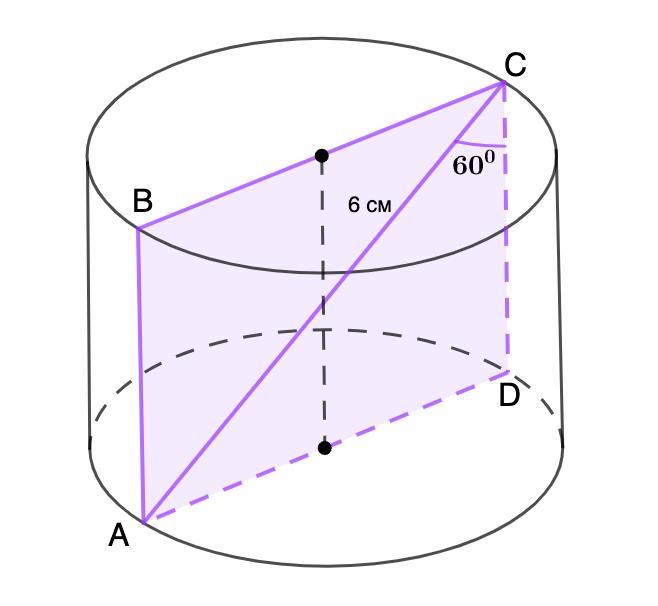
ABCD - осевое сечение;
АС = 6 см; ∠ACD = 60°.
Найти: Sполн.
Решение:
- Осевое сечение - прямоугольник.
Рассмотрим ΔACD - прямоугольный.
- Сумма острых углов прямоугольного треугольника равна 90°.
∠СAD = 90°-60°=30°
- Катет, лежащий против угла 30°, равен половине гипотенузы.
CD=AC:2=6:2=3 (см)
По теореме Пифагора:
AD²=AC²-CD²=36-9=27
AD=3√3 (см)
⇒ диаметр основания равен 3√3 см.
(см)
Найдем площадь полной поверхности:
S полн. = S бок. + 2Sосн. = 2πR·h+2πR² = 2πR (R+h)
h=CD=3 см
(см²)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: настя2695
Предмет: Русский язык,
автор: натабусыгина
Предмет: Русский язык,
автор: Аноним
Предмет: История,
автор: MartinK