Предмет: Алгебра,
автор: Pods556
Помогите найти производные
Приложения:
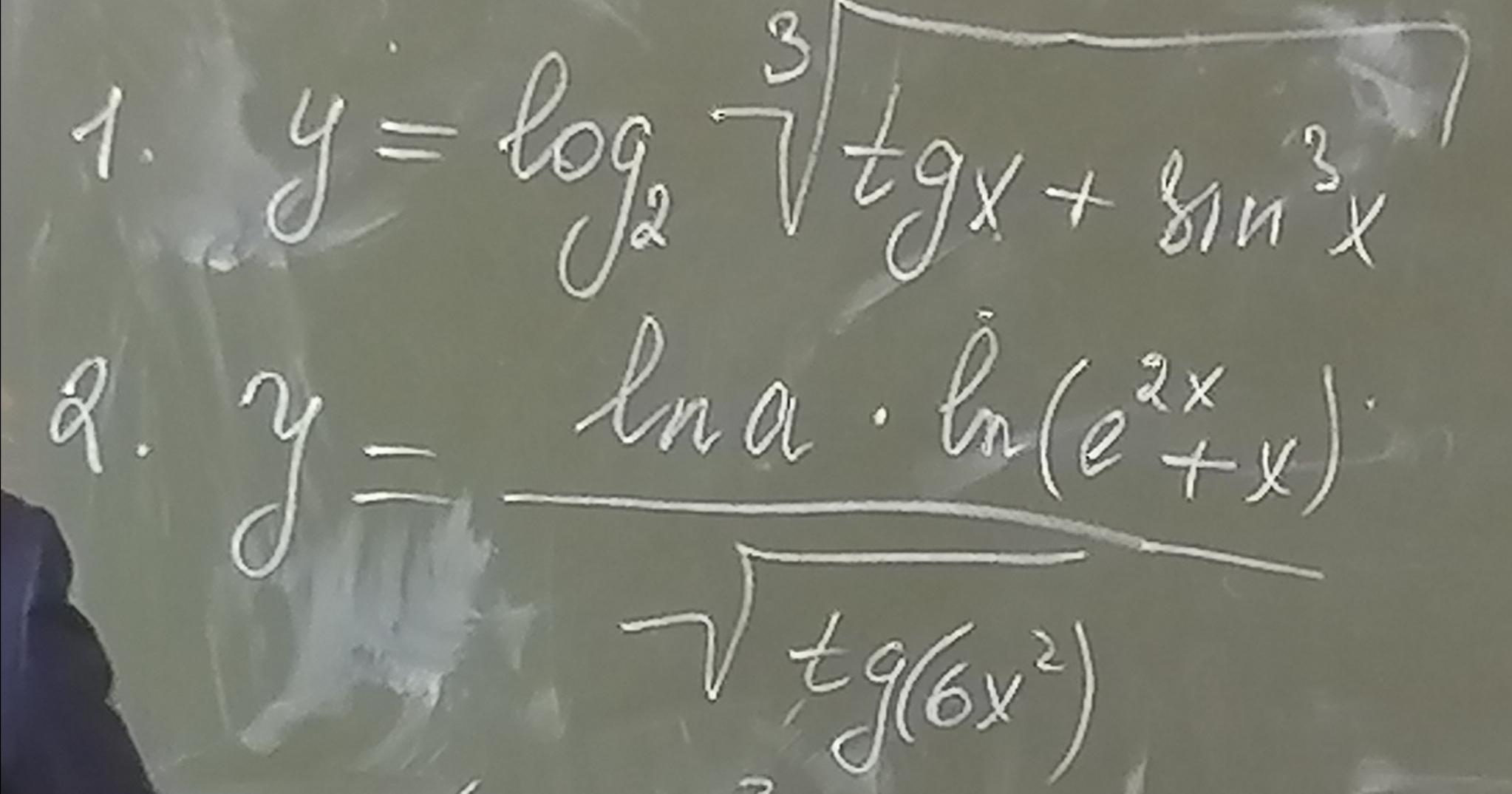
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: tatyanabelousova
Предмет: Русский язык,
автор: Fahtoy
Предмет: Русский язык,
автор: Аноним
Предмет: География,
автор: нураТОР
Предмет: Русский язык,
автор: scat2005