Предмет: Математика,
автор: Аноним
Помогите решить 50 баллов
Приложения:
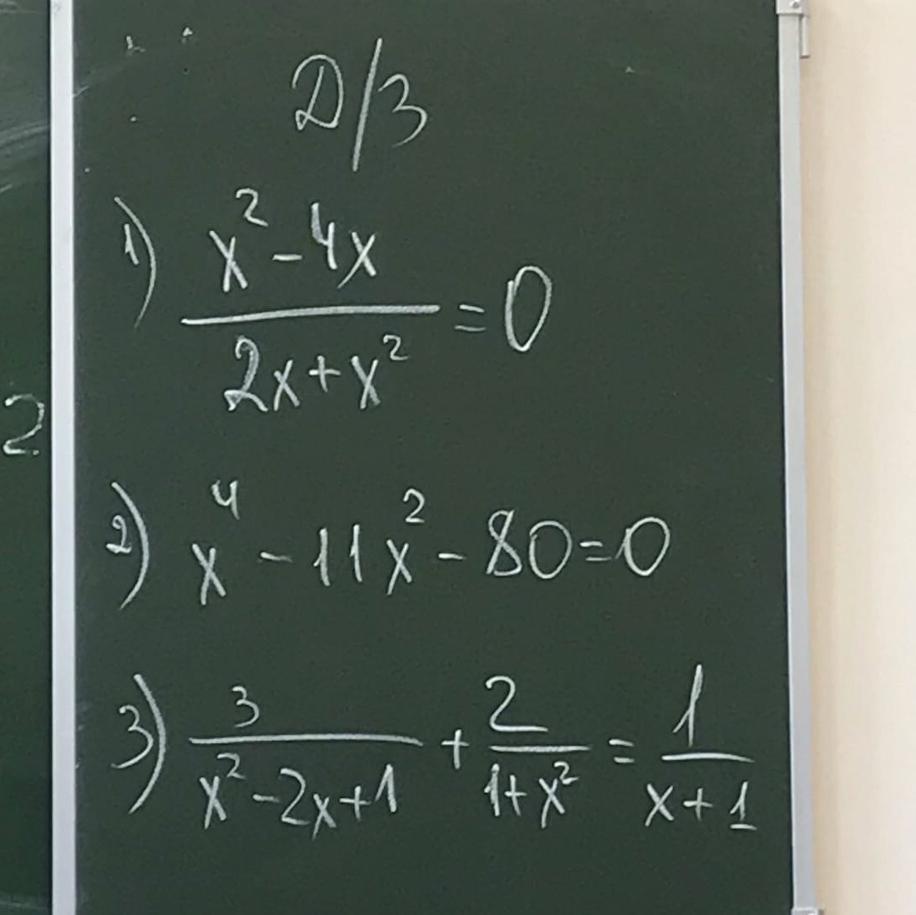
Ответы
Автор ответа:
1
Ответ:
1);
2) ;
3) .
Пошаговое объяснение:
1)
Ответ: Х=4, т.к. Х=0 не удовлетворяет условиям уравнения.
2)
Произведем замену: Пусть ; Тогда,
По т.Виета
находим корни данного уравнения :
, что не удовлетворяет условиям уравнения, значит
3) !!! Вероятно в знаменателе 2/(1+х^2) ошибка. Адекватно решается при знаке "-" в нем. Иначе, корни уравнения будут явно не в виде значений школьной программы.
является общим знаменателем.
Значит
Приведем дробь к общему знаменателю:
По т.Виета находим корни данного уравнения :
не удовлетворяет условиям уравнения.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: ваня548
Предмет: Английский язык,
автор: yrkirillova
Предмет: Другие предметы,
автор: Kate101007
Предмет: Биология,
автор: Аноним