Предмет: Алгебра,
автор: mvolturi
3 примера по тригонометрии
Приложения:
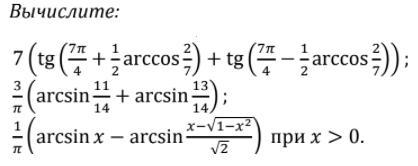
Ответы
Автор ответа:
2
Ответ: -49
Ответ: 2
x\in (0;1]⇒ Рассмотрим
(
такой, что
Поскольку
Ответ:
Замечание. Мы использовали формулы
если
если
Похожие вопросы
Предмет: Українська мова,
автор: glinskad
Предмет: Русский язык,
автор: вторые
Предмет: Русский язык,
автор: 181988
Предмет: Українська мова,
автор: Даеиялка
Предмет: Математика,
автор: Пуся678