Предмет: Алгебра,
автор: vitaliych09
Помогите решить домашнее задание 9 клас
Приложения:

Ответы
Автор ответа:
0
1 задание
2 задание (а)
ответ:
[-2; 3]
2 задание (б)
ответ:
(-2; 1)U(1; +бесконечность)
2 задание (в)
ОДЗ: 2+x≠0, x≠-2
ответ:
(-бесконечность; -2)U(-2; 3]
2 задание (г)
ОДЗ: x ≠ 0
ответ:
-2 < x < 1, x ≠0
(-2; 0)U(0; 1)
3 задание (а)
3 задание (б)
4 задание
Ответ: -1; 3
Приложения:

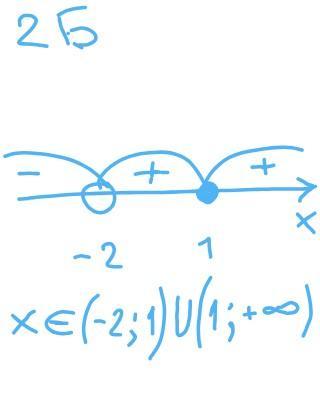
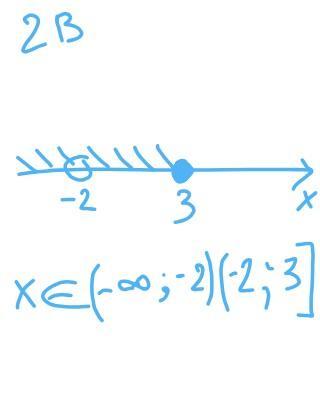
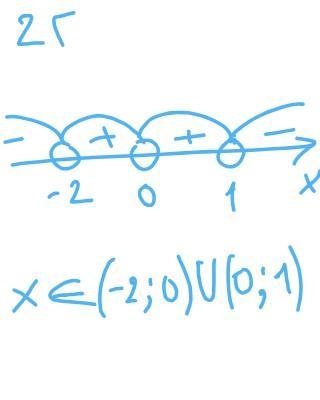
bbbapho:
стоп. у меня ошибки. сейчас иисправлю.
всё, готово.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: marinalidya201
Предмет: Английский язык,
автор: zhogol2003
Предмет: Математика,
автор: Зенитовец228337
Предмет: Другие предметы,
автор: giniatovalilia