Найти множество значений функции. Напишите пожалуйста с подробным решением
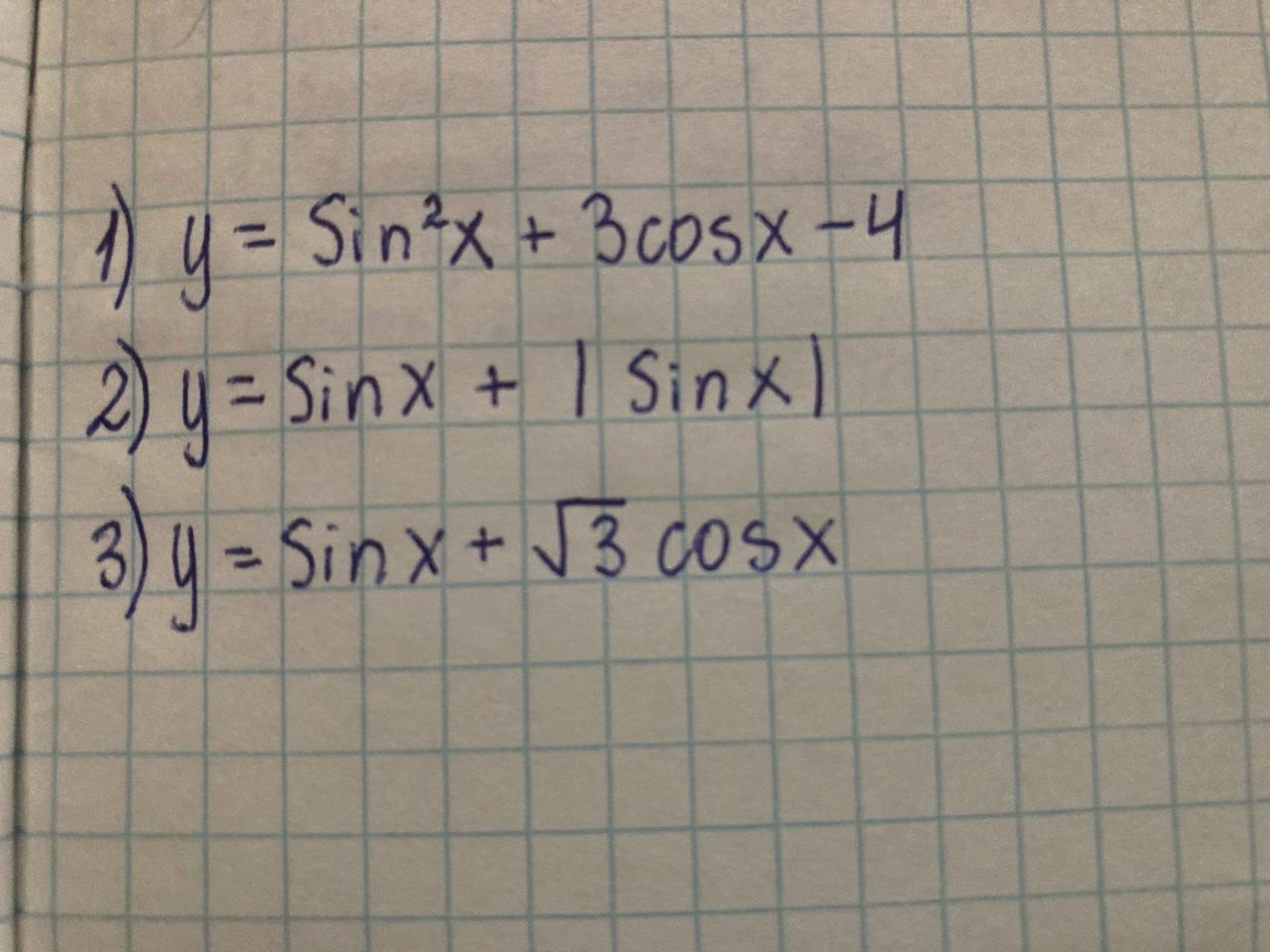
Ответы
Решение:
1)
y = sin² x + 3 cos x - 4
y = 1 - cos²x + 3cos x - 4
y = -cos²x + 3cos x - 3
y' = 2cos x · sin x - 3sin x
y' = sin x · (2cos x - 3)
2cos x - 3 ∈ (-5; -1)
то есть 2cos x - 3 < 0
y' = 0
sin x = 0
точки экстремумов
х = 0; π; 2π; 3π или х = πn
При х = 0 + 2πn у = -1 + 3 - 3 = -1 - максимальное значение
При х = π + 2πn у = -1 - 3 - 3 = -7 - минимальное значение
у ∈ [-7; -1]
2)
y = sin x + |sin x|
sin x ∈ [-1; 1]
|sin x| ∈ [0; 1]
При х ∈ [0 + 2πn; π+2πn] y∈ [0; 2] половинки синусоид складываются
При х ∈ (π +2πn; 2π+2πn] y = 0 половинки синусоид взаимно уничтожаются
у ∈ [0; 2]
3)
y = sin x + √3 · cos x
y' = cos x - √3 · sin x
y' = 0
cos x = √3 · sin x
tg x = 1/√3
точки экстремумов
x = π/6; 7π/6; 13π/6; 19π/6 . . .
При х = π/6+ 2πn у = 0,5 + √3 · 0,5√3 = 2 (максимальное значение)
При х = 7π/6 + 2πn у = -0,5 - √3 · 0,5√3 = -2 (минимальное значение)
у ∈ [-2; 2]