Предмет: Алгебра,
автор: Аноним
Помогите, пожалуйста, срочно!
Найти общее решение или общий интеграл дифференциального уравнения.
Решить задачу Коши.
Приложения:
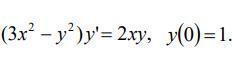
Ответы
Автор ответа:
1
Ответ:
Так как получили решение при х≠0 , то найти частное решение при у(0)=1 невозможно .
Например, если бы задали у(1)=2, то
Похожие вопросы
Предмет: Английский язык,
автор: ника260179
Предмет: Английский язык,
автор: liza469
Предмет: Английский язык,
автор: алина1253
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: BigBlackCat