Предмет: Алгебра,
автор: Аноним
Помогите, пожалуйста, срочно! Исследовать функцию z = z( x, y) на экстремум
Приложения:
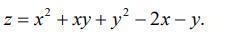
Ответы
Автор ответа:
1
Ответ:
Функция имеет экстремум который является минимумом в точке (1;0) и
Объяснение:
Функция имеет экстремум
https://znanija.com/task/45300460?answeringSource=feedPublic%2FhomePage%2F3
С этим я вряд ли смогу помочь
Или же завтра уже напишу решение
Похожие вопросы
Предмет: Английский язык,
автор: ageorginova
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: Efsane94
можешь, пожалуйста, тут помочь