ПРОШУ ПОМОГИТЕ!!!! Я НЕ ПОНИМАЮ!!!(((
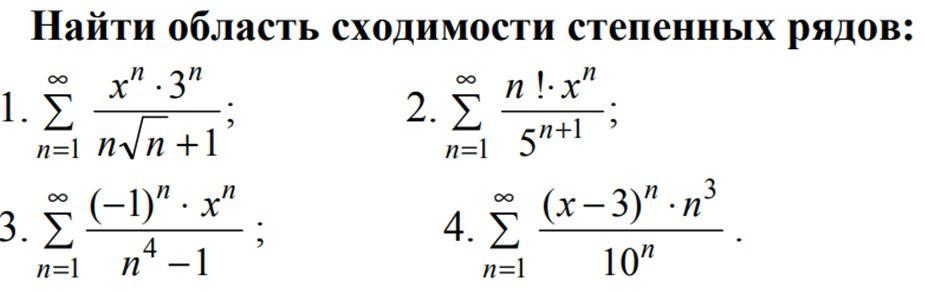
Ответы
Ответ:
Пошаговое объяснение:
область сходимости степенного ряда определяется величиной радиуса сходимости R (при условии R >0)- это интервал (-R; R), где , на границах интервала сходимость ряда исследуется отдельно
все наши ряды имеют вид , мы работаем с аₙ
итак, поехали
1)
- вычислим радиус сходимости
тогда ряд является абсолютно сходящимся при х ∈ (-1/3;1/3)
- теперь исследуем поведение ряда на концах интервала
а) точка x = -1/3 подставим x = -1/3 в наш ряд, получим числовой ряд
'это у нас знакочередующийся ряд. исследуем его по признаку Лейбница
-- по первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, для нашего ряда возьмем первые три члена ряда - это условие выполняется
-- по второму признаку Лейбница предел ряда должен стремится к 0. тоже у нас выполняется
чтобы говорить об абсолютной или условной сходимости, необходимо исследовать ряд по одному из признаков сходимости рядов. мы применим сравнительный признак
как уже упрощали выше, у нас получился обобщенный гармонический ряд с α> 1 , он сходится, значит и наш числовой ряд сходится абсолютно, а из этого следует, что наш исходный ряд в точке х= -1/3 сходится.
б) точка х = 1/3. подставим в исходный ряд, получим числовой ряд
- это обычный числовой ряд. его надо исследовать на сходимости при помощи признака сходимости ряда - мы используем сравнительный признак. это мы уже проделывали выше, получали обобщенный гармонический ряд с α> 1, отсюда вывод - и наш числовой ряд сходится абсолютно, а из этого следует, что наш исходный ряд в точке х= 1/3 сходится.
ответ
таким образом мы установили, что исходный степенной ряд является сходящимся при x ∈ [-1/3; 1/3]
2) найдем радиус сходимости ряда
ответ
степенной ряд сходится абсолютно при x=0
4)
- считаем радиус сходимости
теперь найдем х₁ =3-10 = -7 х₂ =3+10 =13
тогда ряд сходится абсолютно при x ∈ (-7;13)
- теперь проверим сходимость ряда на концах этого интервала
а) точка х = -7 подставим, получим числовой ряд
это знакочередующийся ряд. и у него не выполняется первый признак Лейбница 1 < 8 < 27 - этот ряд расходится. значит и наш степенной ряд в точке х=-7 расходится
б) точка х = 13 подставим и получим числовой ряд
это у нас положительный ряд и по сравнительному признаку он расходится (n³ = 1/n⁻³ α <1), а это значит, что и наш степенной ряд в точке х=13 расходится
ответ
степенной ряд сходится при x∈ (-7;13)
3) посчитаем радиус сходимости
ряд сходится на интервале (-1;1)
дальше аналогично тому, как делали выше, надо исследовать на концах интервала.
после исследования получим
степенной ряд сходится при x∈ (-1;1]