Предмет: Математика,
автор: kuznetsovam82
Помогите решить пожалуйста срочно!!!
Приложения:
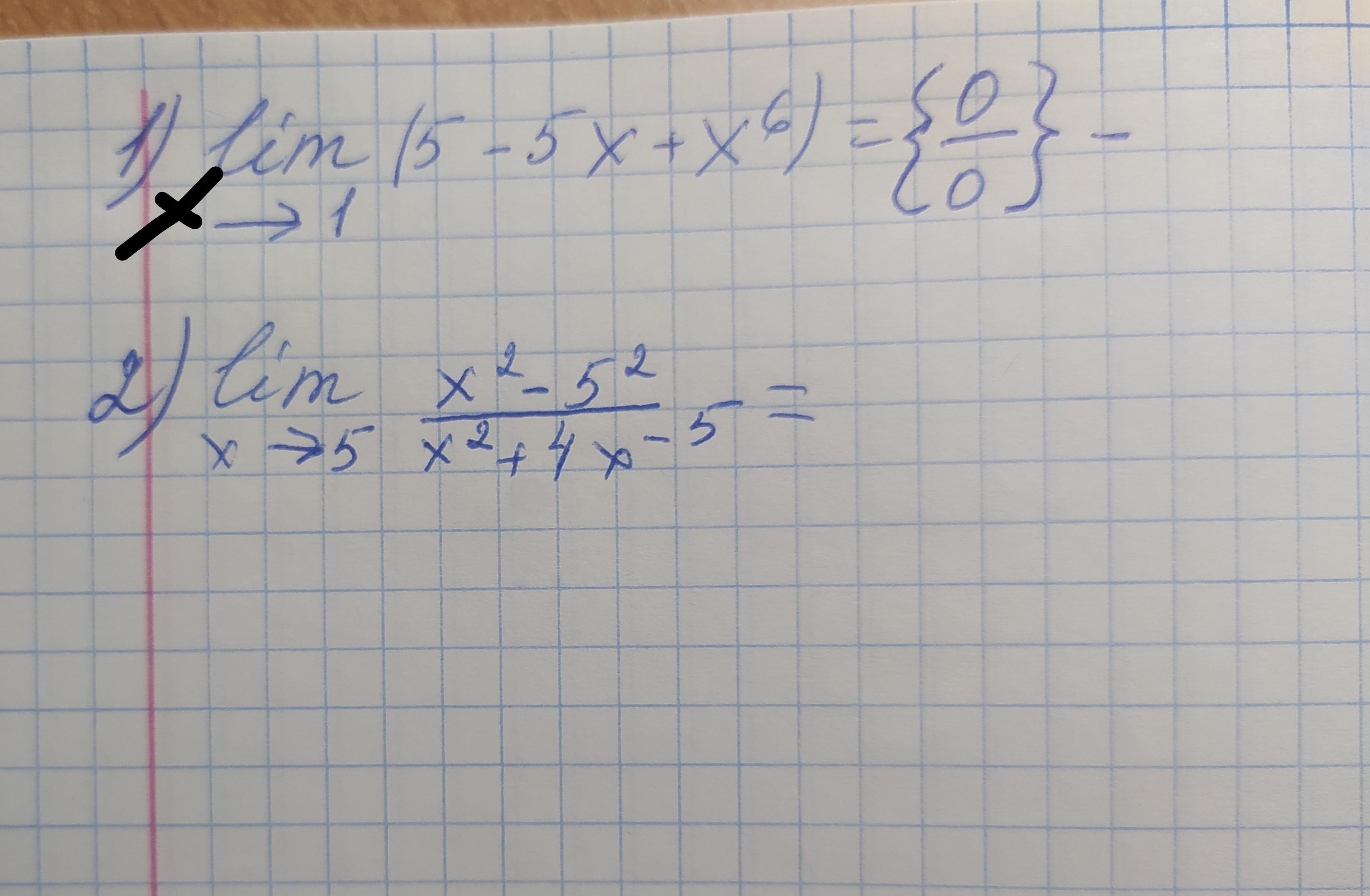
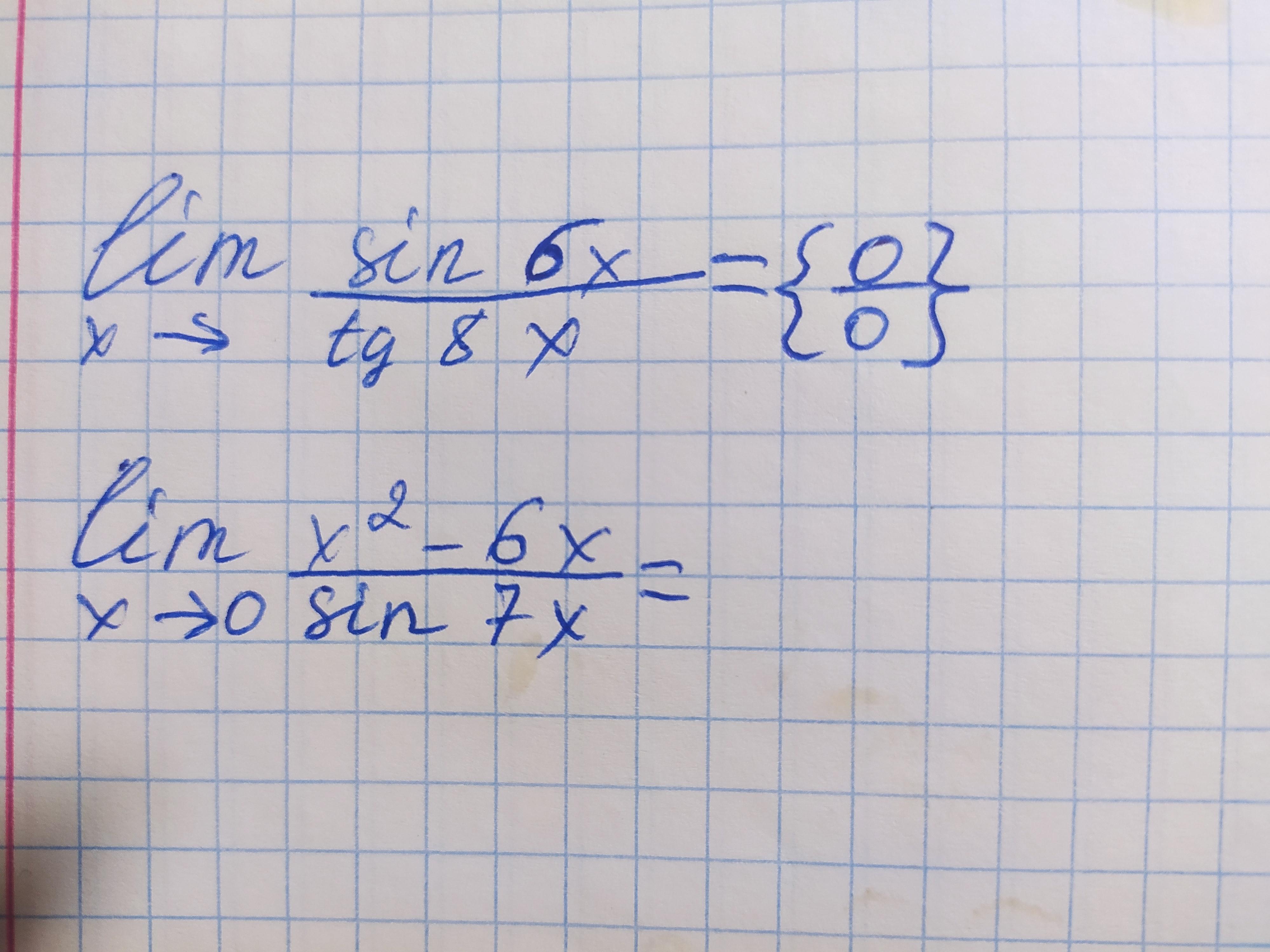
Ответы
Автор ответа:
1
Ответ:
1;0;-;-6/7
Пошаговое объяснение:
1) Никакой неопределенности как написано в тетради нет, поэтому просто подставляем 1 вместо x
2) Никакой неопределенности также нет, в знаменателе получился не ноль при подстановке, поэтому опять просто подставляем
3) Не написано к чему стремится x
4) В данном пределе при x->0 sin(7x) ~ 7x (Первый замечательный предел)
Похожие вопросы
Предмет: Русский язык,
автор: ростислав10
Предмет: Другие предметы,
автор: даша020904
Предмет: Русский язык,
автор: rocklee213
Предмет: Английский язык,
автор: Okeyyy1
Предмет: Українська мова,
автор: Jeve