Предмет: Алгебра,
автор: Аноним
Помогите, пожалуйста, срочно!
Найди угол между градиентами функции u (x, y, z) и v (x, y, z) в точке М.
Приложения:
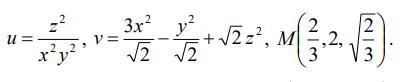
Ответы
Автор ответа:
1
Ответ:
Аноним:
можешь помочь с заданиями, которые я выложила, пожалуйста!
Похожие вопросы
Предмет: Русский язык,
автор: баха22
Предмет: Русский язык,
автор: NYAKAWAII4
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: svetik151088x
Предмет: История,
автор: 4444Андрей16111