Предмет: Геометрия, автор: s0807

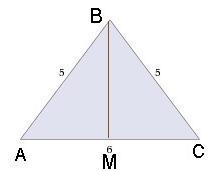
В треугольнике АВС медиана ВМ, равная 4 см, является высотой. биссектриса СN пересекает сторону ВМ в точке К
Найдите: отрезок КМ

Приложения:

Simba2017: MC^2=BC^2-BM^2=5^2-4^2=9; MC=3

Simba2017: биссектриса делит ВМ пропорционально прилегающим сторонам

Simba2017: KM=3x; KB=5x; 3x+5x=4; x=0.5; KM=3*0.5=1.5

s0807: спасибо, мне еще одно решение подсказали, найти радиус вписанной окружности

Simba2017: да, можно и так...

Аноним: S = ah/2 = 6 * 4/2 = 12
S = pr => r = S/p = 12*2/(5+5+6) = 1.5

Аноним: KM = r

Ответы

Автор ответа: Аноним

Поскольку ΔABC - равнобедренный, то BM - медиана, высота и биссектриса. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

KM = r.

AM = MC = AC/2 = 3 см. По теореме Пифагора (ΔABM):

BM = √(AB² - AM²) = 4 см

S = ah/2 = 6 * 4/2 = 12 см². С другой стороны S = pr

KM = r = S/p = 2S/P = 2*12/(5+5+6) = 1.5 см

Ответ: 1.5 см.

Примечания: p - полупериметр треугольника, P - периметр тр-ка.

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Русский язык, автор: MashaSpok0011

От основы слова в рамке Образуйте прилогательное вот слово))) "За плечо"

Срочно..плизз...