Предмет: Геометрия,
автор: s0807
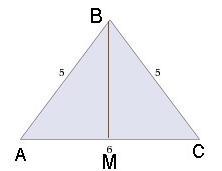
В треугольнике АВС медиана ВМ, равная 4 см, является высотой. биссектриса СN пересекает сторону ВМ в точке К
Найдите: отрезок КМ
Приложения:
mathkot:
Вы уверены в условии задачи?
То, что я вижу сейчас, то в численном виде получить длину KM невозможно.
Поэтому у меня вопросы к условию
да уверена. а почему не возможно?
А теперь возможно, просто после того как вы добавили рисунок появились дополнительные данны
а да я забыла его сначала. буду очень благодарна если решите, я получила два совсем разных ответа и сломала себе мозг
Сейчас решу.
Ответы
Автор ответа:
1
Ответ:
см
Объяснение:
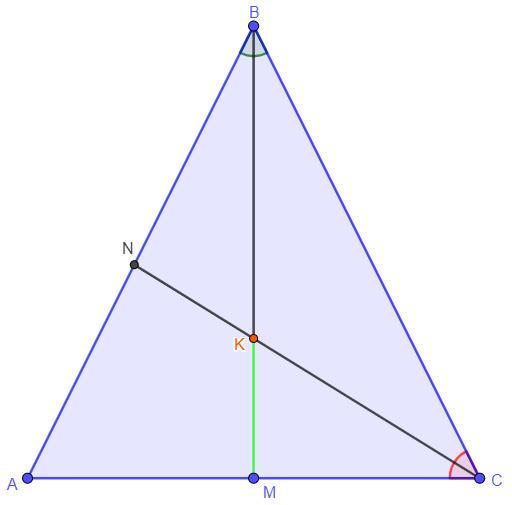
Дано: BM - медиана, биссектриса; CN - биссектриса, AB = BC = 5 см,
AC = 6 см
Найти: KM - ?
Решение: Так как по условию BM - медиана, то AM = MC = AC : 2 = 6 : 2 = 3 см. Так как по условию AB = BC, то треугольник ΔABC - равнобедренный. Так как треугольник ΔABC - равнобедренный, то медиана проведенная к основанию является высотой и биссектрисой по теореме. Треугольник ΔCMB является прямоугольным так как
BM ⊥ AC. BM = BK + KM ⇒ BK = BM - MK = 4 - MK.
Так как по условию CN - биссектриса, то по теореме о биссектрисе для треугольника ΔCMB:
см.
Приложения:
Решение понятно?
Да, спасибо большое)
Похожие вопросы
Предмет: Русский язык,
автор: никитка25
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: sergeyromanovich
Предмет: Биология,
автор: Abdulloeffali
Предмет: Английский язык,
автор: katerina42784637