Question

Высоты треугольника АВС пересекаются в точке Н.Найдите углы АНВ,ВНС,СНА,если угол А=50°,уголВ=60°​

Answer 1

Ответ:

∠АНВ = 110°

∠ВНС = 130°

∠СНА = 120°

Объяснение:

Сумма углов треугольника равна 180°.

Сумма острых углов прямоугольного треугольника равна 90°.

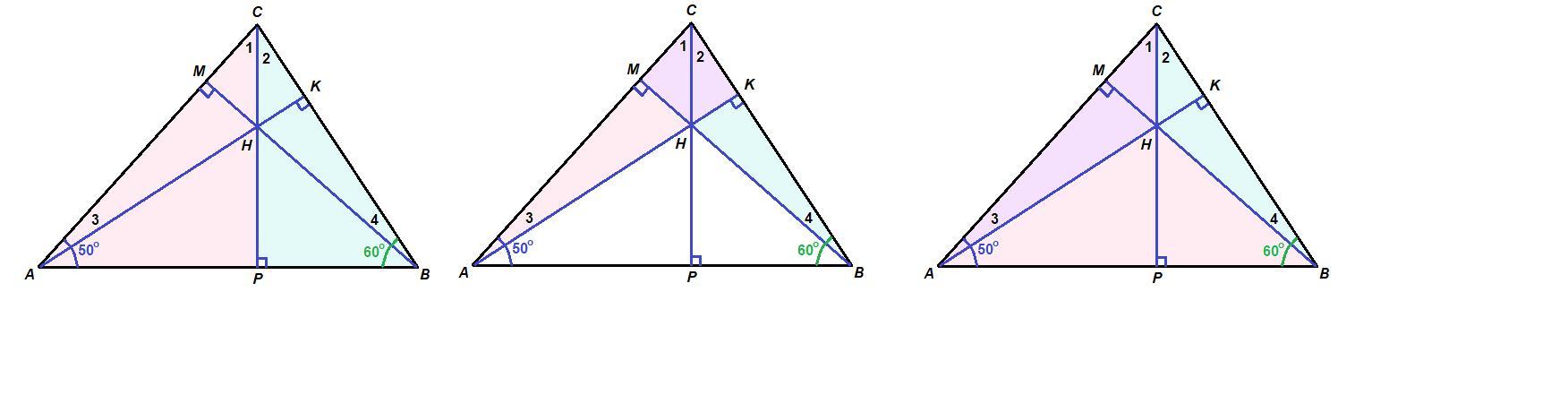
Рисунок 1:

ΔАСР:   ∠АРС = 90°, ∠САР = 50°,  значит

 ∠1 = 90° - 50° = 40°

ΔВСР:   ∠ВРС = 90°,  ∠СВР = 60° , значит

 ∠2 = 90° - 60° = 30°

∠АСВ = ∠1 + ∠2 = 40° + 30° = 70°

Рисунок 2.

ΔАСК:  ΔАКС = 90°,  ∠АСК = 70°, значит

∠3 = 90° - 70° = 20°

ΔВСМ:   ∠ВМС = 90°,   ∠ВСМ = 70°, значит

∠4 = 90° - 70° = 20°

∠НАВ = ∠САВ - ∠3 = 50° - 20° = 30°

∠НВА = ∠СВА - ∠4 = 60° - 20° = 40°

Рисунок 3.

ΔАНВ:

∠АНВ = 180° - (∠НАВ + ∠НВА) = 180° - (30° + 40°) = 180° - 70° = 110°

ΔВНС:

∠ВНС =  180° - (∠2 + ∠4) = 180° - (30° + 20°) = 180° - 50° = 130°

ΔСНА:

∠СНА = 180° - (∠1 + ∠3) = 180° - (40° + 20°) = 180° - 60° = 120°