Предмет: Геометрия,
автор: Lalalal43
кут при вершині першого рівнобедреного трикутника 45°, його площа 25√2 см. Знайти бічні сторони трикутника.
Ответы
Автор ответа:
0
Ответ:
10 см
Объяснение:
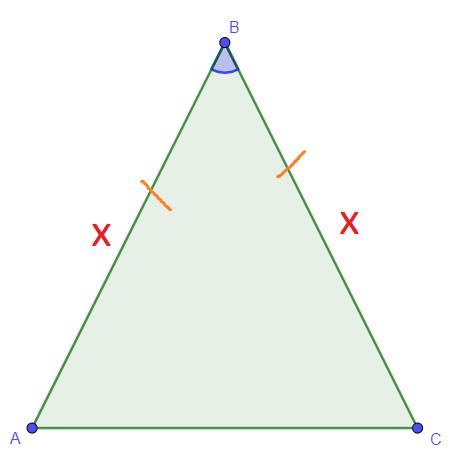
Дано: AB = BC, см², ∠ABC = 45°
Знайти: AB,BC - ?
Розв'язання: Нехай AB = x, тоді BC = x так як за умовою AB = BC. За формулою площі трикутника:
(x > 0, так як х сторона трикутника)
см.
AB = BC = x = 10 см.
Приложения:
Похожие вопросы
Предмет: Українська література,
автор: Аноним
Предмет: Қазақ тiлi,
автор: даша1877
Предмет: Русский язык,
автор: Ляман5
Предмет: Окружающий мир,
автор: ласка12
Предмет: Русский язык,
автор: vladekb1