Предмет: Геометрия,
автор: skrabdlyatela
Прямая AC — касательная к окружности с центром Ој, а пря-
имая BD — касательная к окружности с центром О, Докажите, что: а) AD || BC; б) АВ2 = AD. BC; в) BD2 : AC2 = AD: BC.
Приложения:
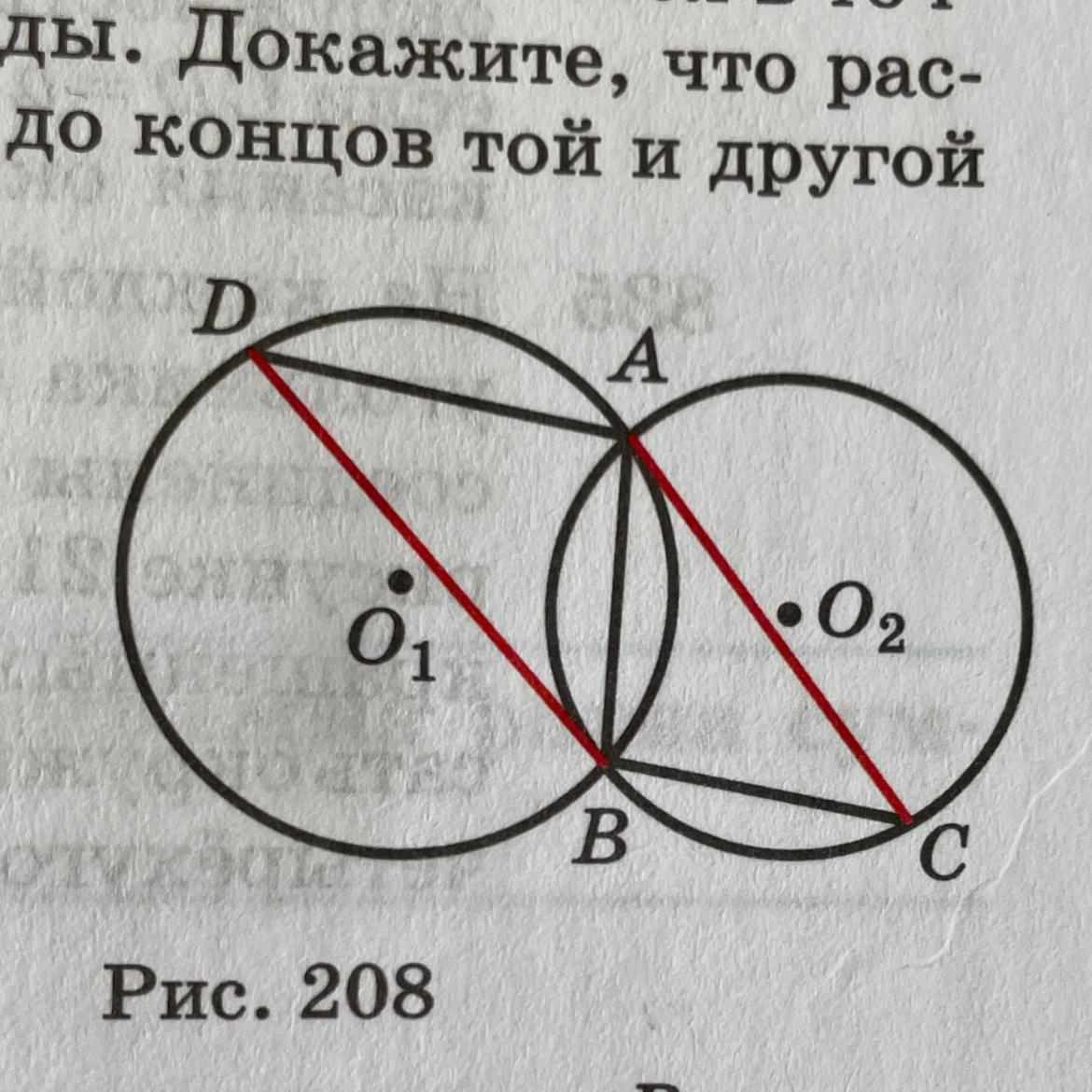
Ответы
Автор ответа:
0
AC - касательная к окружности О1
BD - касательная к окружности О2
Докажите
а) AD||BC
б) АВ^2 = AD*BC
в) BD^2:AC^2 = AD:BC
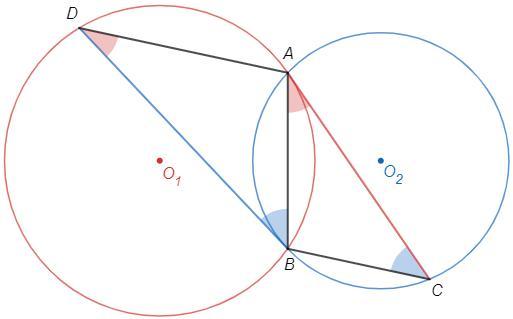
Угол между касательной и хордой равен половине дуги, стягиваемой хордой.
∠CAB=∠ADB=∪AB/2 (красная)
∠DBA=∠BCA=∪BA/2 (синяя)
△DAB~△ABC (по двум углам)
a) ∠DAB=∠ABC => AD||BC (т.к. накрест лежащие углы равны)
б) AB/BC =AD/AB => AB^2 =AD*BC
в) BD/AC =AD/AB; BD/AC =AB/BC
BD/AC *BD/AC =AD/AB *AB/BC => BD^2/AC^2 =AD/BC
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: rodionovvitalik
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Окружающий мир,
автор: jaleasadova063
Предмет: Математика,
автор: Некииорвоцщ