Предмет: Алгебра,
автор: Аноним
упростите выражение срочноо❤️❤️❤️❤️❤️❤️❤️
Приложения:
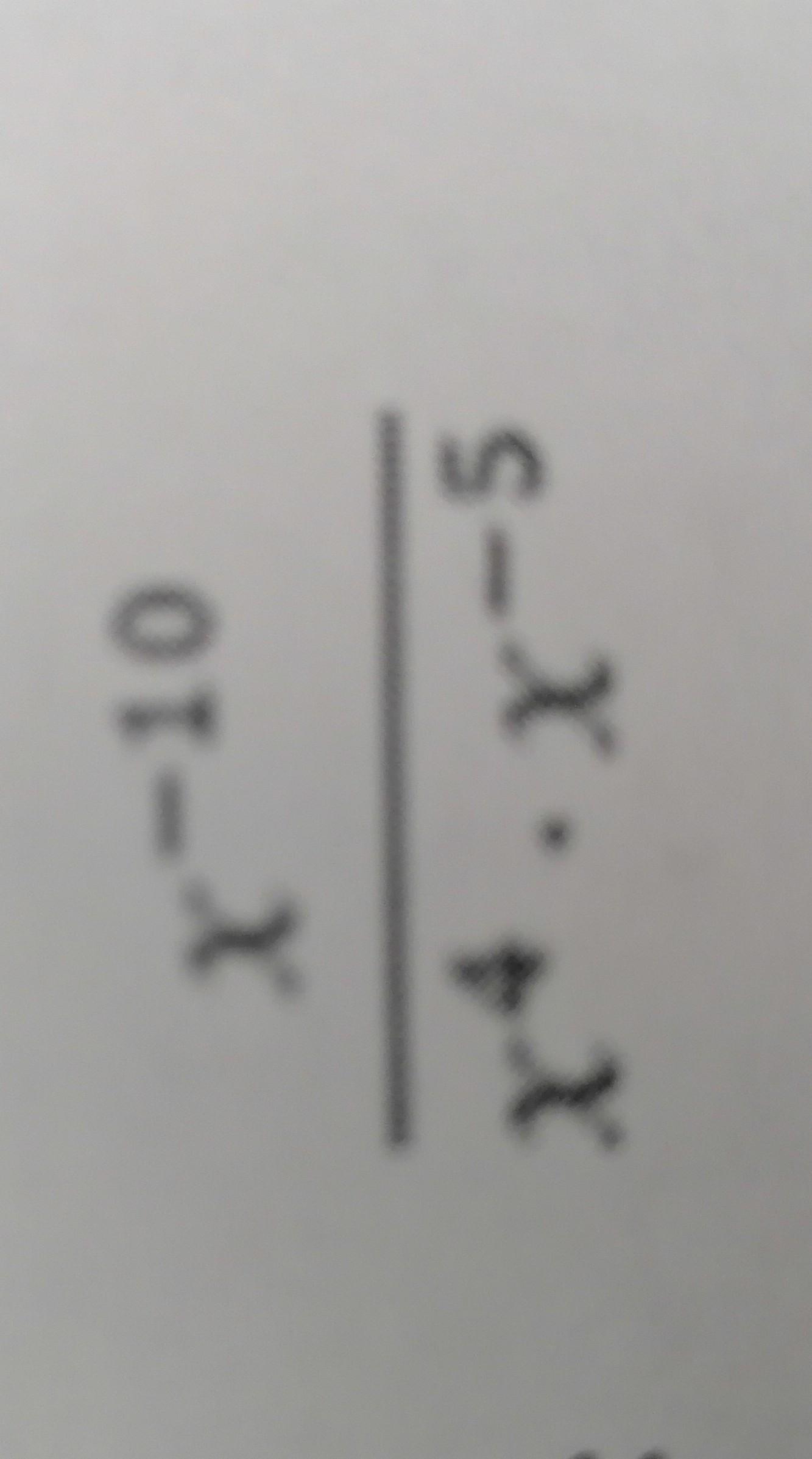
Ответы
Автор ответа:
0
х⁻¹⁰ : (х⁴ * х⁻⁵)=х⁻¹⁰ : (х⁴⁻⁵)=х⁻¹⁰ : х⁻¹=х⁻¹⁰⁻⁽⁻¹⁾=х⁻¹⁰⁺¹=х⁻⁹=1/х⁹.
Привыкните, можно коротко:
х⁻¹⁰⁻⁴⁻⁽⁻⁵⁾=х⁻⁹.
При делении показатели вычитаем.
Аноним:
Спасибо за ЛО))
Автор ответа:
0
Ответ:
.
Объяснение:
Нам дан пример:
Число в отрицательной степени, это дробь, в которой в числителе будет 1, а в знаменателе наше число, но уже в положительной степени.
Поэтому, разберем сначала знаменатель:
- мы преобразовали второе значение переменной согласно правилу выше, и сократили числитель и знаменатель по степени.
Теперь, возвращаясь в исходный пример, получим:
Преобразуем числитель по правилу выше:
Теперь, по правилу деления одной дроби на другую, вторую дробь мы переворачиваем и умножаем их между собой:
- это и будет итоговый ответ на наш пример.
Похожие вопросы
Предмет: Английский язык,
автор: жансок1
Предмет: Қазақ тiлi,
автор: Banka4ik
Предмет: Қазақ тiлi,
автор: alinkabananka2004
Предмет: Қазақ тiлi,
автор: Настяzet
Предмет: Математика,
автор: Саша36281