Question

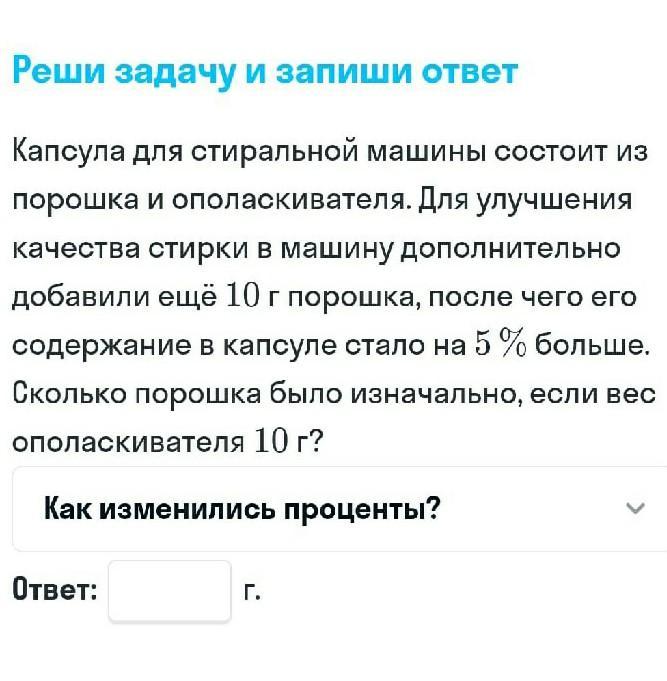
Ужас как срочно надо,прмогите пожалуйста​

Answer 1

Ответ:

30 г порошка было изначально

Пошаговое объяснение:

Пусть порошка изначально было х г. Ополаскивателя 10 г. Значит всего капсула весит (х+10) г.

Изначальное соотношение порошка и всего ополаскивателя было равно

$\frac{x}{x+10}$ .

После добавления 10 г порошка получаем всего порошка в капсуле (х+10) г. А всего капсула весит (х+10)+10=х+20 г.

Значит соотношение порошка и капсулы здесь равно

$\frac{x+10}{x+20}$.

По условию задачи порошок во втором соотношении увеличился на 5%. То есть на 0,05.

Получаем уравнение

$\frac{x}{x+10}+0,05=\frac{x+10}{x+20}$

$\frac{x+0,05(x+10)}{x+10}=\frac{x+10}{x+20}$

$\frac{1,05x+0,5}{x+10}=\frac{x+10}{x+20}$

Приведем к общему знаменателю.

$(1,05x+0,5)(x+20)}=(x+10)^2$

Раскроем скобки

1,05х²+0,5х+21х+10=х²+20х+100

1,05х²-х²+21,5х-20-х+10-100=0

0,05х²+1,5х-90=0

D=1,5²-4*(-90)*0,05=2,25+4*90*0,05=2,25+18=20,25=4,5²

$x_{1,2}=\frac{-1,5\pm4,5}{2*0,05}$

$x_{1,2}=\frac{-1,5\pm4,5}{0,1}$

Отрицательный корень не подходит по смыслу задачи. Остается только положительный.

х=10*(-1,5+4,5)

х=10*3

х=30 г - порошка было изначально в капсуле.