Предмет: Алгебра,
автор: sssirosssi
10 КЛАСС ПОМОГИТЕ С ПРИМЕРАМИ ПЛИЗ✌ 70 баллов!!
Приложения:
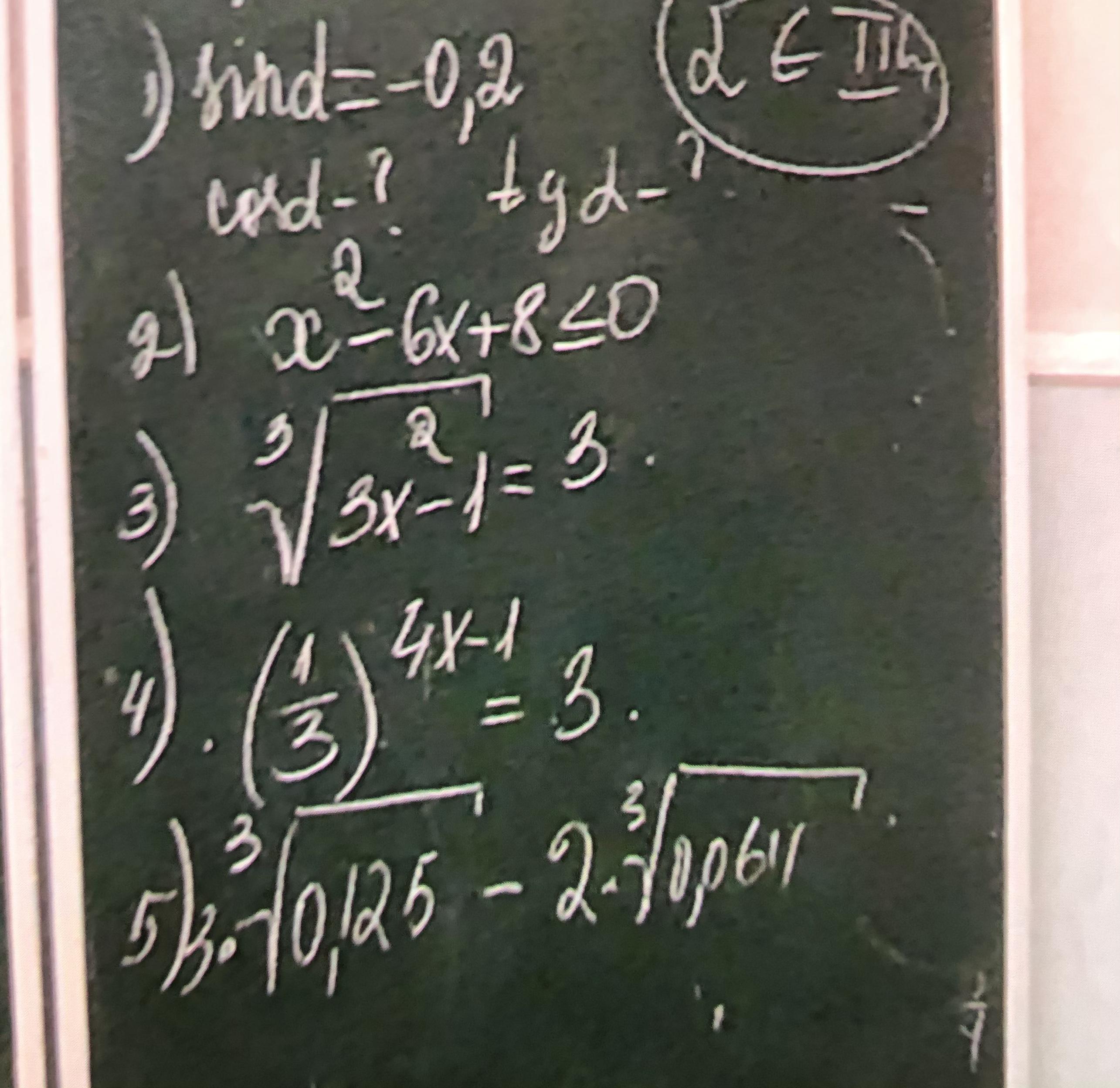
Ответы
Автор ответа:
1
1) α - угол третьей четверти, значит Cosα < 0 , tgα > 0 .
+ + + + + [2] - - - - -[4] + + + + +
////////////////
Ответ : x ∈ [2 ; 4]
Похожие вопросы
Предмет: Другие предметы,
автор: katya1357924680
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: fidarova65
Предмет: Литература,
автор: sashamenkov17