Question

Помогите, пожалуйста, срочно!
Используя преобразование координат, построить кривую. Указать
координаты центра в новой системе координат, а также полуоси кривой.

Answer 1

$9x^2+4y^2-54x-32y+109=0 \\ 9x^2-54x+4y^2-32y+109=0\\ 9(x^2-6x)+4(y^2-8y)+109=0 \\ 9(x^2-6x+9-9)+4(y^2-8y+16-16)+109=0 \\ 9((x-3)^2-9)+4((y-4)^2-16)+109=0 \\ 9(x-3)^2-81+4(y-4)^2-64+109=0 \\ 9(x-3)^2+4(y-4)^2=36 \ |:36 \\ \\ \frac{(x-3)^2}{4} +\frac{(y-4)^2}{9} =1$

Замена: $x-3=\widetilde{x}; \ y-4=\widetilde{y}$

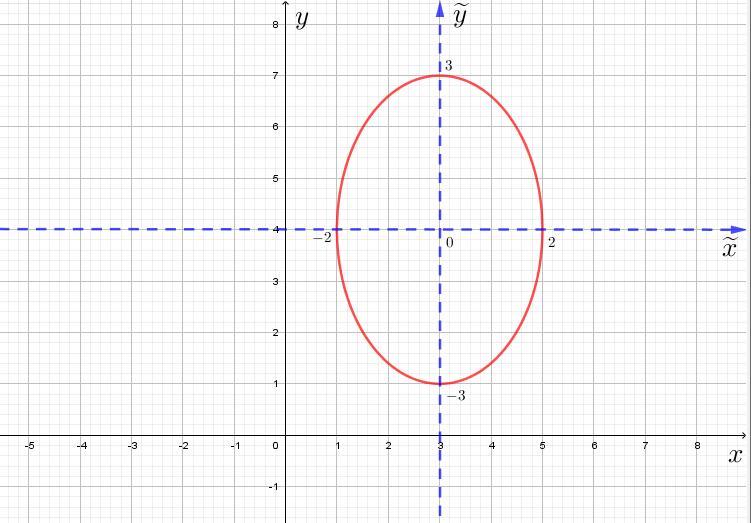
$\frac{\widetilde{x}}{4} +\frac{\widetilde{y}}{9} =1$ - каноническое уравнение эллипса

Центр (3;4)

Полуоси: a=√4=2;  b=√9=3