Предмет: Алгебра,
автор: sofiaslepicko
найдите наибольшее значение дроби
Приложения:
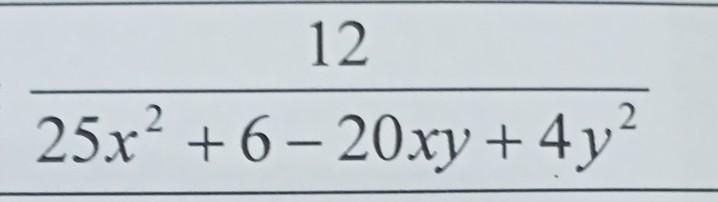
Ответы
Автор ответа:
0
Ответ:
Наибольшее значение дроби равно 2
Объяснение:
Эта дробь имеет наибольшее значение при наименьшем знаменателе.
Наименьший знаменатель равен 6 при условии 5х - 2у = 0. Тогда
Похожие вопросы
Предмет: Русский язык,
автор: Ах4ейшен
Предмет: Другие предметы,
автор: Анжелика15л
Предмет: Русский язык,
автор: loxpesKekpek
Предмет: Русский язык,
автор: mindumelena
Предмет: Английский язык,
автор: Андрей3241