Question

х²-2,1|х|+1,1=0
Помогите пожалуйста ​

Answer 1

Ответ:

x₁ = 1; x₂ = 1,1; x₃ = –1; x₄ = –1,1

Объяснение:

x² – 2,1|x| + 1,1 = 0

1) x ≥ 0

x² – 2,1x + 1,1 = 0

x₁ = 1; x₂ = 1,1 (по формулам Виета)

Оба корня удовлетворяют условию x ≥ 0.

2) x < 0

x² + 2,1x + 1,1 = 0

x₃ = –1; x₄ = –1,1 (по формулам Виета)

Оба корня удовлетворяют условию x < 0.

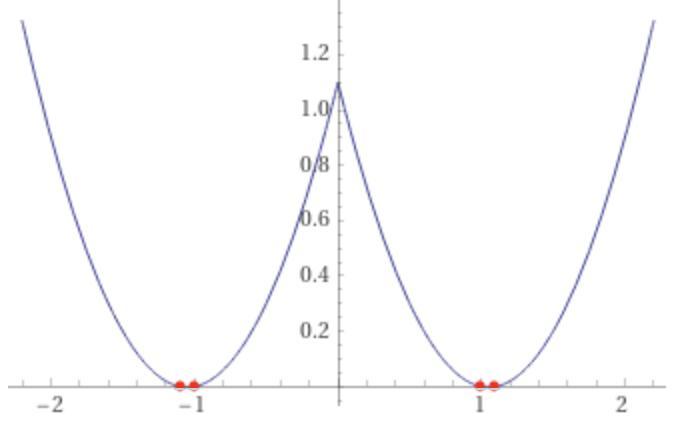
Второй возможный подход к решению – заметить, что график y = x² – 2,1|x| + 1,1 симметричен относительно OY. Далее решить уравнение без модулей, отбрасывая получившиеся отрицательные корни (если они будут), и потом для каждого положительного корня дописать еще один с обратным знаком.

Answer 2

$x^{2} -2,1|x|+1,1=0\\\\x^{2}=|x|^{2}\\\\|x|=m, \ m\geq0\\\\m^{2}-2,1m+1,1=0\\\\Teorema \ Vieta:\\\\m_{1}=1,1\\\\m_{2} =1\\\\1) \ |x|=1,1\\\\x_{1} =1,1 \ ; \ x_{2} =-1,1\\\\2) \ |x|=1\\\\x_{3}=1\\\\x_{4}=-1\\\\Otvet:\boxed{1,1 \ ; \ -1,1 \ ; \ 1 \ ; \ -1}$