Предмет: Алгебра,
автор: holdikgey8
Дан треугольник, стороны которого 10 см, 6 см, 8 см. Найти периметр треугольника, вершинами которого являются середины сторон данного треугольника.
Milena17:
Надо найти периметр данного треугольника Р=10+6+8=24 см. Теперь находим периметр серединного треугольника, он равен половине заданного треугольника, то есть 24:2=12 см
Ответы
Автор ответа:
7
Ответ:
12см
Объяснение:
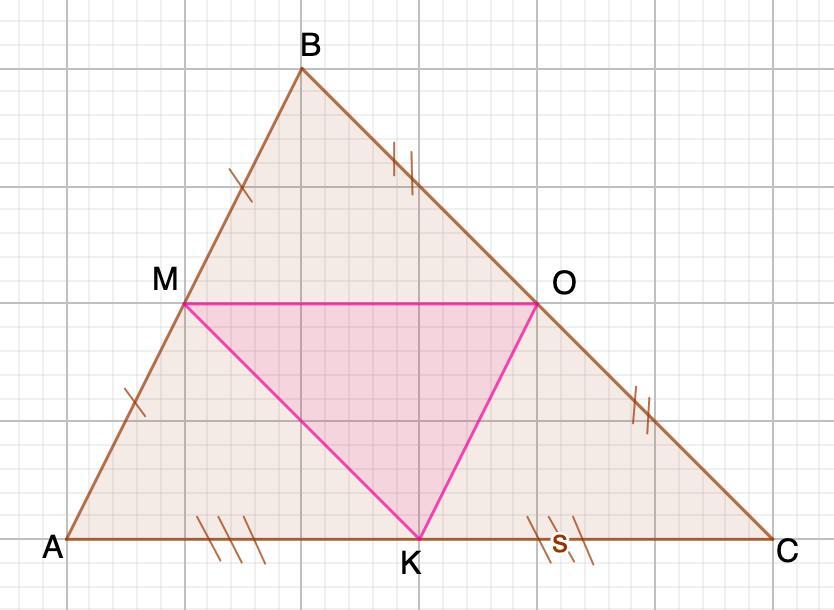
Дано: ΔАВС
АС=10 см; ВС=8 см; АВ=6 см.
АМ=МВ; ВО=ОС; АК=КС.
Найти: Р ΔМОК.
Решение:
Отрезок, соединяющий середины сторон треугольника - средняя линия.
МО - средняя линия.
ОК - средняя линия.
КМ - средняя линия.
По свойству средней линии:
Найдем периметр ΔМОК:
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: Кетиноар
Предмет: Русский язык,
автор: gladkova0606
Предмет: Русский язык,
автор: KsuhaMatuhina
Предмет: Русский язык,
автор: ЧерныйКот78
Предмет: Русский язык,
автор: keonencore