Предмет: Геометрия,
автор: asaliya22012007
помогите пожалуйста
Приложения:

Ответы
Автор ответа:
2
Ответ:
Объяснение:
Дано:
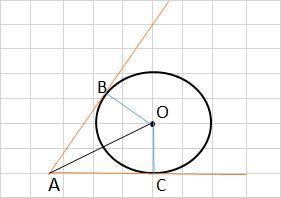
АВ, АС - касательные к окружности с центром в т. О
∠ВАС = 60°
r - ?
Решение:
1) Соединим любую из точек касания В (С) с центром окружности О.
ВО (СО) - радиусы окружности.
Теорема 1: Касательная к окружности перпендикулярна радиусу, проведённому в точку касания,т.е.
АС ⊥ОС (АВ ⊥ОВ)
2) Теорема 2. Прямая, проходящая через центр окружности и точку, из которой исходят касательные, делит угол между касательными пополам, т.е.
∠ВАО = ∠ОАС = ∠ВАС/2 = 60°/2 = 30°
3) ΔОАС - прямоугольный (АС ⊥ОС ) и ∠ОАС = 30°.
Теорема 3. В прямоугольном Δ-ке против угла в 30° лежит катет, равный половине гипотенузы:
ОС = АО / 2 = 16/2 = 8(см)
r = ОС = 8см
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: katcornewa
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Русский язык,
автор: СёвенокАрина
Предмет: Математика,
автор: tokhtakulieva
Предмет: Математика,
автор: ximiojo7779