Question

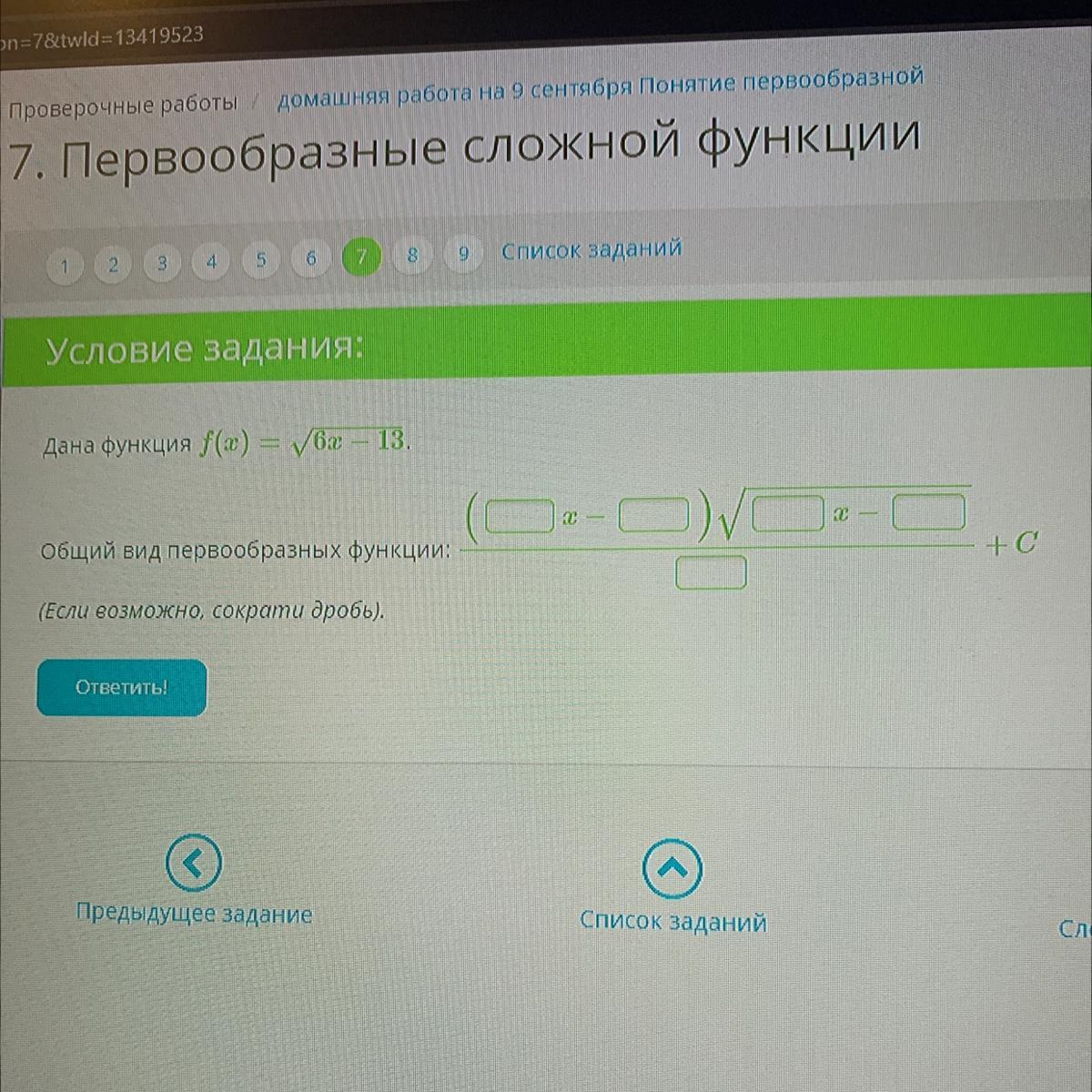
нужно найти общий вид первообразной функции

Answer 1

Ответ:

Пошаговое объяснение:

сначала я найду семейство первообразных (общий вид первообразной) а потом преобразую это так, чтобы было возможно записать в требуемую форму ответа

$\displaystyle \int {\sqrt{6x-13} } \, dx =\left[\begin{array}{ccc}u=6x-13\\du=6dx\hfill\\\end{array}\right] =\frac{1}{6} \int {\sqrt{u} } \, du =\frac{1}{6} *\frac{2u^{3/2}}{3} +C=\\\\=\frac{(6x-13)^{3/2}}{9} +C=\qquad \boldsymbol {(1)}\\\\=\frac{\sqrt{(6x-13)^3} }{9} +C= \frac{(6x-13)\sqrt{6x-13} }{9} +C\qquad \boldsymbol {(2)}$

вот, выбирайте форму ответа (1) или (2). они равнозначны.

(2) - это как надо записать в указанную форму,