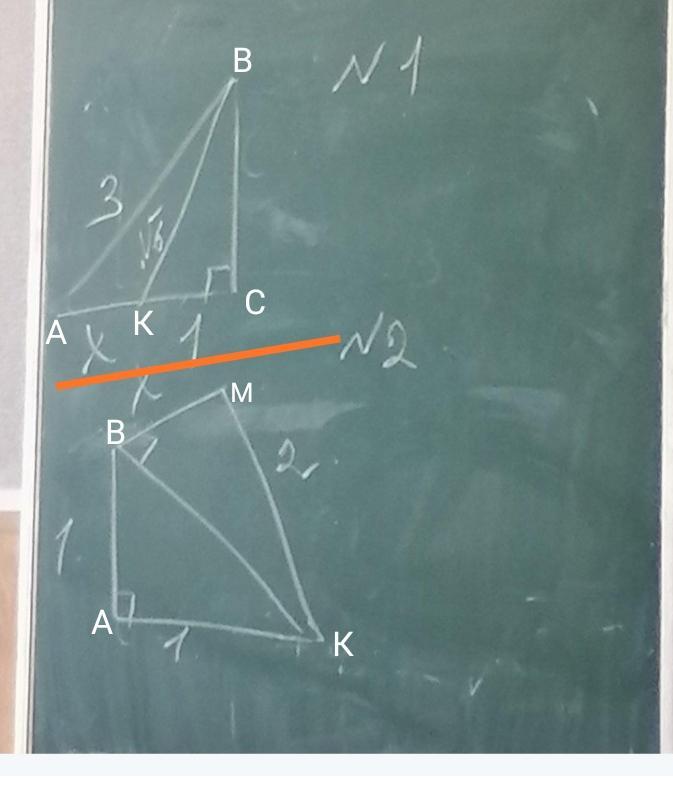
Помоги мне пожалуйста с этим (фото). Я вообще ничего не понимаю по геометрии

Ответы
Ответ:
Zmeura1204
Объяснение:
1)
∆КВС- прямоугольный треугольник
По теореме Пифагора
ВС=√(ВК²-КС²)=√((√6)²-1²)=√(6-1)=√5 ед
∆АВС- прямоугольный треугольник
По теореме Пифагора
АС=√(АВ²-ВС²)=√(3²-(√5)²)=√(9-5)=√4=
=2 ед.
АК=АС-КС=2-1=1 ед.
Ответ: х=1 ед.
2)
∆ВАС- прямоугольный равнобедренный треугольник.
ВК=АК*√2=√2 ед.
∆ВМК- прямоугольный треугольник
По теореме Пифагора
ВМ=√(МК²-ВК²)=√(2²-(√2)²)=√(4-2)=√2 ед.
Ответ: х=√2 ед.
Ответ:
Объяснение:
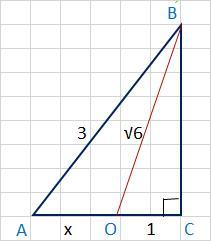
1. ∠С отмечен квадратиком, это означает, что он прямой, т.е ∠С =90°. Значит, ΔАВС и ∠ОВС - прямоугольные
(Гипотенуза - это сторона Δ-ка, лежащая против прямого угла)
2. Теорема, необходимая для решения задач с прямоугольным треугольником:
Квадрат гипотенузы равен сумме квадратов катетов, т.е.
АВ² = ВС² + АС² ( из ΔАВС) и
ОВ² = ВС² + ОС² (из ΔОВС)
3. Решение
а) Рассмотрим ΔОВС.
ОВ² = ВС² + ОС² или
(√6)² = ВС² + 1², откуда
ВС² = 6-1
ВС² = 5
б) теперь обратимся к ΔАВС.
АВ² = ВС² + АС² или
3² = 5 +АС², откуда
АС² = 9 -5 = 4
АС = √4 = 2
Но АС = АО + ОС или
2 = АО + 1
АО = х = 2 -1
АО = х = 1
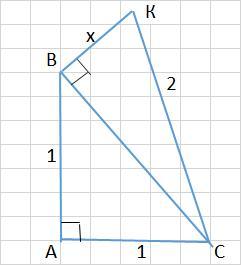
№2.
1) ΔАВС - прямоугольный, т.к. ∠А = 90° (прямой)
ВС² = АВ² + АС² (квадрат гипотенузы = сумме квадратов катетов)
ВС² = 1 + 1
ВС² = 2
2) Рассмотрим ΔВКС, он тоже прямоугольный, т.к. ∠КВС = 90° (по условию, рис.)
КС² = ВС² +ВК² или
2² = 2 + х²
х ² = 4 - 2
х² = 2
х = √2