Предмет: Математика,
автор: asskifss
решите уравнение:

Ответы
Автор ответа:
3
Ответ:
Пошаговое объяснение:
это биквадратное неравенство
будем решать через замену
положим 2x² = z
тогда получим обычное квадратное неравенство
z² -z -1 ≥ 0
корни уравнения z² -z -1 = 0
поскольку это парабола ветвями вверх, то ≥ 0 она будет при
далее возвращаемся к нашей замене
2х² не может быть ≤ отрицательного числа.
поэтому мы берем корень z₂ и делаем обратную замену
таким образом получим ответ
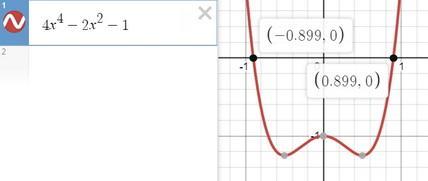
для проверки посмотрим на график и убедимся, что решение наше правильное.
при этом помним, что на графике рассматриваем область, где
функция ≥ 0 соответственно выбираем область для х
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: иринка63
Предмет: Русский язык,
автор: Айша111111111
Предмет: Другие предметы,
автор: Vikalencemars
Предмет: Қазақ тiлi,
автор: нубик19
Предмет: История,
автор: ksrinasuper