Предмет: Алгебра,
автор: krylovisnasta
Решите пожалуйста, очень срочно!!!!
Приложения:
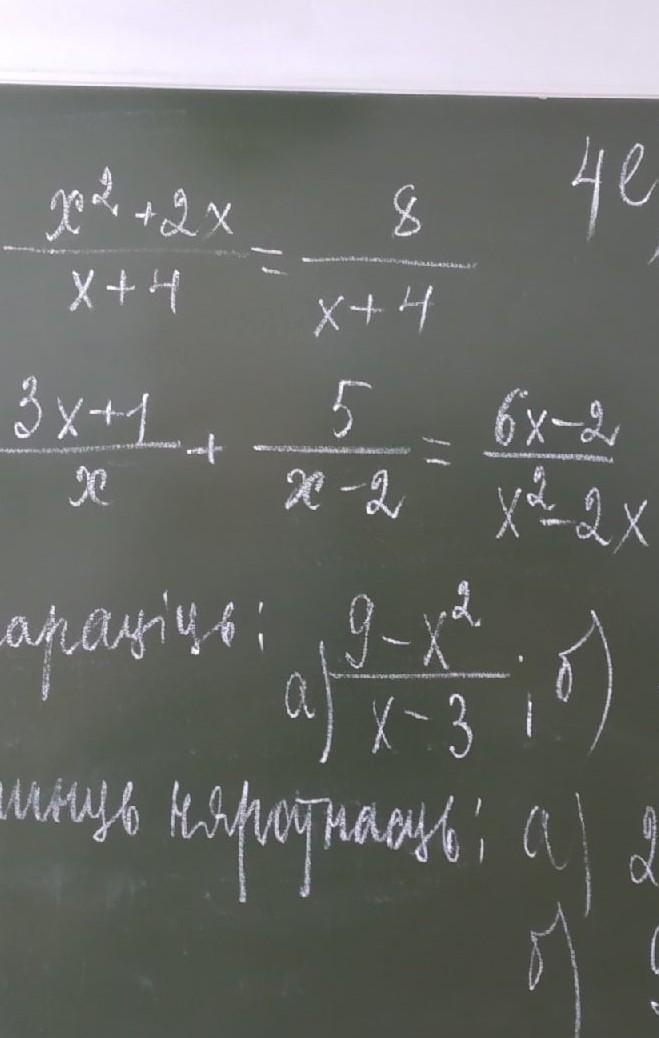
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Українська мова,
автор: EgorioLaL
Предмет: Английский язык,
автор: Maxson4x
Предмет: Английский язык,
автор: milkamilkamilka1
Предмет: Математика,
автор: Mila13121
Предмет: Русский язык,
автор: мадина595