Предмет: Алгебра,
автор: bilmansofia
помогите решить ,дам 15 баллов
Приложения:
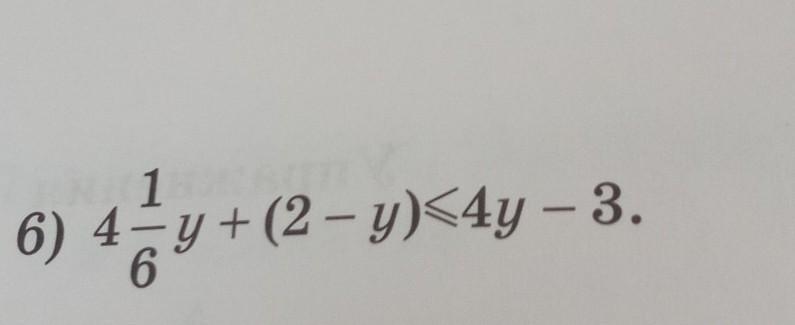
Ответы
Автор ответа:
1
Ответ:
y ≥ 6
Объяснение:
Автор ответа:
2
Ответ:
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: tomani22
Предмет: Английский язык,
автор: leman6
Предмет: Английский язык,
автор: сайпу
Предмет: Математика,
автор: батаник72
Предмет: Математика,
автор: BorinDub