Вариант 2 В задании
№ 1 выберите один верный ответ. № 1. Если один из смежных углов равен 98°, то второй угол будет 1 )прямой 2) острый 3)развернутый 4)тупой
№2 Какое из следующих утверждений верно? Запишите их номера. 1) Если угол равен 54°, то вертикальный с ним равен 126°. 2) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие тре- угольники равны. 3)Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна 180°, то прямые параллель- 11 НЫ. K
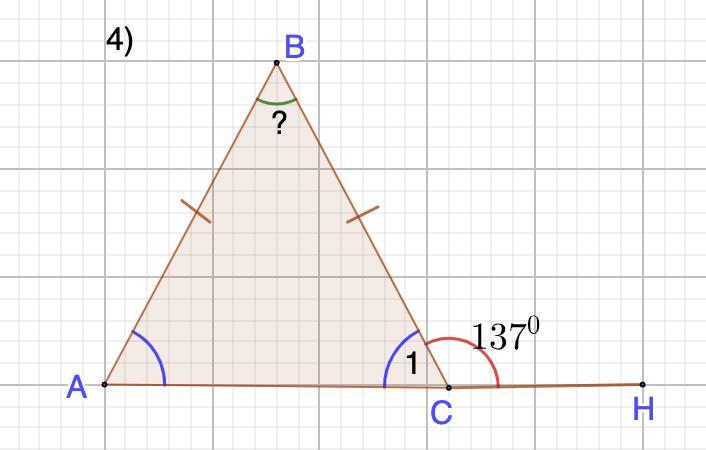
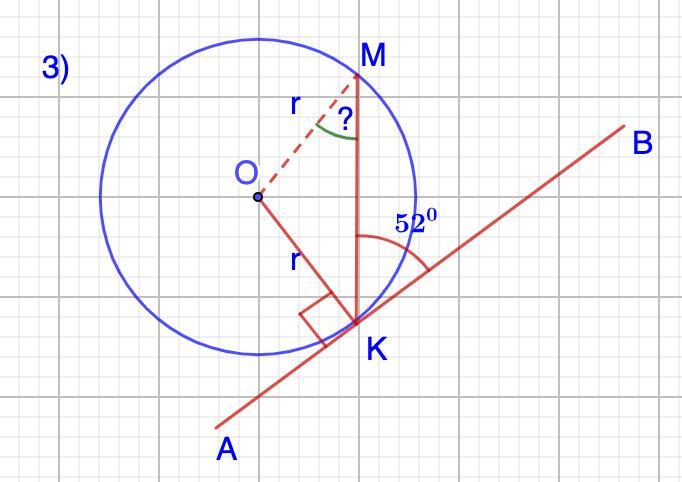
№3 Прямая касается окружности в точке К. Точка 0 — центр окружности. Хорда КМ образует с касательной угол, равный 52°. Найдите величину угла ОМК. Ответ дайте в градусах. №4 В треугольнике ABC AB = BC. Внешний угол при верши- не с равен 137°. Найдите угол В. Ответ дайте в градусах.
№5. В равнобедренном треугольнике один из углов равен 120°, высота, проведенная к основанию 8 см. Найдите боковую сторону.
срочно!!! отдам все баллы

Ответы
Объяснение:
1.
Смежные углы в сумме равны 180°.
Если один угол равен 98°, то второй будет равен:
180°-98°=82°
82°<90° ⇒ угол острый.
2.
1) Если угол равен 54°, то вертикальный с ним равен 126°.
НЕВЕРНО.
Вертикальные углы равны.
2) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
ВЕРНО.
Это второй признак равенства треугольников.
3) Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна 180°, то прямые параллельны.
ВЕРНО.
Это один из признаков параллельности прямых.
3.
Дано: Окр. Or;
АВ - касательная; КМ - хорда; ∠МКВ=52°.
Найти: ∠ОМК.
Решение:
∠ОКВ=90° (радиус, проведенный в точку касания, ⊥ касательной)
⇒∠ОКМ=90°-52°=38°
ΔКОМ - равнобедренный (КО=ОМ=r)
⇒ ∠ОКМ=∠ОМК=38° (углы при основании равнобедренного Δ-ка равны)
4.
Дано: ΔАВС - равнобедренный;
∠ВСН=137° - внешний.
Найти: ∠В.
Решение:
∠1=180°-137°=43° (смежные)
∠А=∠1=43° (углы при основании р/б Δ-ка)
∠В=180°-(43°+43°)=94° (сумма углов Δ-ка)
5.
Дано: ΔАВС - равнобедренный.
∠В=120°; ВН=8 см - высота.
Найти: АВ.
Решение:
∠НВС=∠В:2=120°:2=60° (высота в р/б Δ-ке является биссектрисой)
Рассмотрим ΔНВС - прямоугольный.
∠НВС=60° ⇒ ∠С=90°-60°=30° (сумма острых углов п/у Δ-ка)
ВН = 8 см ⇒ ВС=8·2=16 (см) (катет, лежащий против угла 30°)