Предмет: Алгебра,
автор: denprosto86
реши графически систему уравнений {y=x²
{x-y=0
Ответы
Автор ответа:
1
Ответ:
Объяснение:
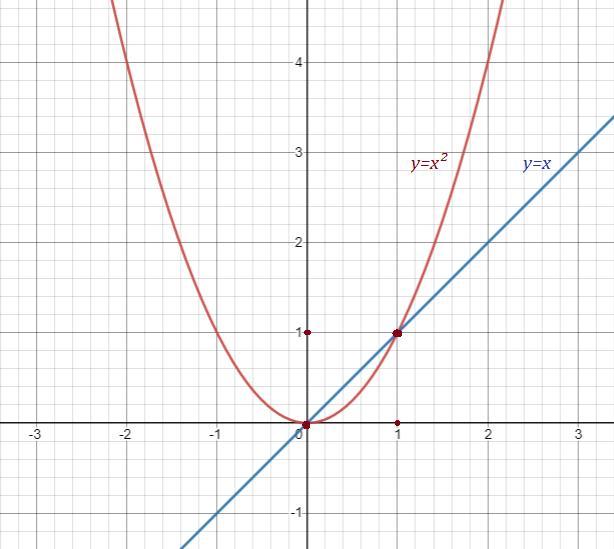
чтобы решить систему уравнений графически на одной и той же системе рисуем два графика и находим точки пересечения
y=x² известная парабола с вершиной (0; 0) ветвями вверх
х-у =0 у = х известная прямая, проходящая через точку (0;0), вторую точку например (1; 1)
в нашем случае система имеет два решения
Приложения:

Автор ответа:
2
Ответ:
Приложения:
qazakalnur03010:
а можете сказать сколько будет {y=x³ {x-y=0
тоже (0,0) и (1,1)
Похожие вопросы
Предмет: Русский язык,
автор: dimiX24
Предмет: Английский язык,
автор: nikatsibuliaeva
Предмет: Русский язык,
автор: tkan4encko2013
Предмет: Русский язык,
автор: ksaqipа
Предмет: Английский язык,
автор: ayka72