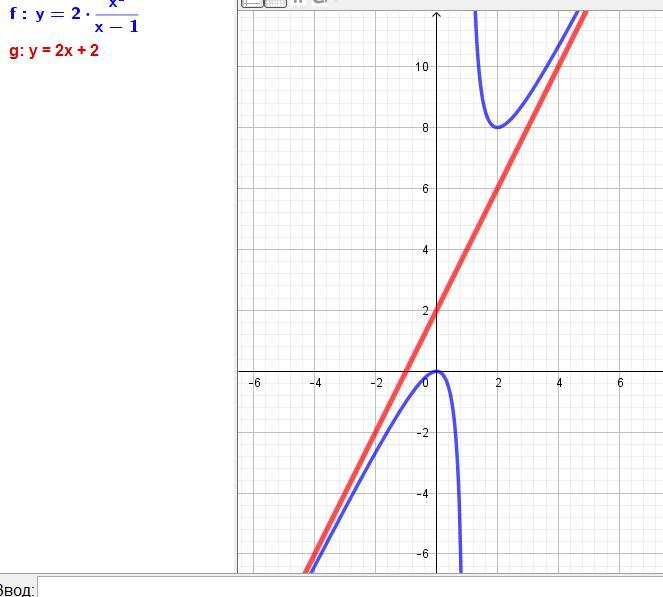
найти асимптоты кривых
y= 2x²/x-1
Ответы
Асимптоты кривой ( это гипербола) y= 2x²/x-1.
Вертикальная асимптота – это прямая х =1, определена как точка разрыва функции.
Горизонтальные асимптоты графика функции:
Горизонтальную асимптоту найдем с помощью предела данной функции при x->+∞ и x->-∞. Соответствующие пределы находим:
lim (2x^2/(x-1)), x->+∞ = ∞, значит, горизонтальной асимптоты справа не существует.
lim (2x^2/(x-1)), x->-∞ = -∞, значит, горизонтальной асимптоты слева не существует.
Наклонные асимптоты графика функции:
Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при lim(x→∞) (kx + b - f(x)).
Находим коэффициент k:
k=lim┬(x→∞)〖〖2x〗^2/(x-1)x=lim┬(x→∞)〖2x/(x-1)=(2x/x)/(x/x-1/x)=2/(1-0)=2〗.〗
Находим коэффициент b:
b=lim┬(x→∞)〖〖2x〗^2/(x-1)-2*x=lim┬(x→∞)〖(〖2x〗^2-〖2x〗^2+2x)/(x-1)=2x/(x-1)=(2x/x)/(x/x-1/x)=2/(1-0)=2〗.〗
Получаем уравнение наклонной асимптоты: y = 2x + 2.