Question

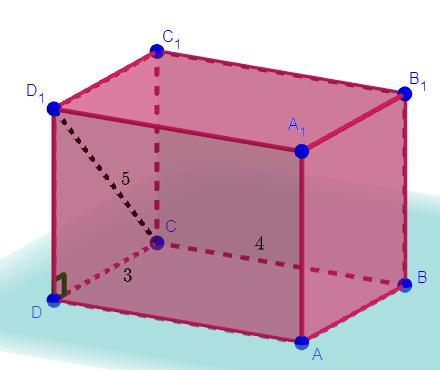
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра CD, CB и диагональ боковой грани CD1 равны соответственно 3,4 и 5. Найдите объём параллелепипеда ABCDA1B1C1D1

Answer 1

Ответ:

Объём параллелепипеда ABCDA₁B₁C₁D₁ равен

48 кубических единиц

Объяснение:

Дано: ABCDA₁B₁C₁D₁ - прямоугольный параллелепипед, CD = 3,

CB = 4, CD₁ = 5

Найти: V - ?

Решение:

По определению прямоугольного параллелепипеда (ABCDA₁B₁C₁D₁ - прямоугольный параллелепипед по условию) все его грани являются прямоугольниками, тогда

СC₁D₁D и ABCD - прямоугольники.

Так как СC₁D₁D - прямоугольник, то по определению прямоугольника все его углы равны 90°, тогда угол ∠D₁DC = 90°.

Рассмотрим треугольник ΔD₁DC.

Так как угол ∠D₁DC = 90°, то треугольник ΔD₁DC - прямоугольный по определению.

По теореме Пифагора:

$DD_{1} = \sqrt{CD_{1}^{2} - CD^{2}} = \sqrt{5^{2} - 3^{2}} = \sqrt{25 - 9} = \sqrt{16} = 4$.

Так как ABCD - прямоугольник, то по свойствам прямоугольника его противоположные ребра равны, тогда CB = AD = 4.

По формуле объем прямоугольного параллелепипеда есть произведение трёх его ребер, выходящих из одной вершины, тогда:

V = DD₁ · AD · CD = 4 · 4 · 3 = 16 · 3 = 48 кубических единиц.

#SPJ3