Решите уравнение

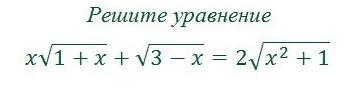
Ответы
Угадываем x=1 ( верно). ОДЗ:
правая часть неотрицательна, поэтому левая часть неотрицательна. Поскольку x=-1 не является решением, делаем вывод, что x неотрицателен. Поэтому возведение в квадрат является на [0;3] равносильным переходом.
x=1 мы и так уже знали; этот корень мы отбрасываем. Остается рассмотреть
Вроде бы все преобразования были равносильны. Но вдруг мы что-то не заметили или допустили арифметическую ошибку. Поэтому попробуем подставить этот корень в уравнение.
ура!
Ответ: 1 и
Замечание. Решение получилось не самое простое. Буду рад, если кто-нибудь придумает более простое решение. Но по любому нужно уметь продираться и через такие выкладки. Кстати, я сначала не заметил замену через t, мне пришлось делать еще одно возведение в квадрат. Получилось уравнение шестой степени, в котором дважды выделялась скобка (x-1), а возникающий многочлен 4-й степени оказался полным квадратом (что, конечно, тоже нужно было увидеть).
Ответ:
Объяснение:
воспользуемся неравенством Коши-Буняковского
причем равенство только если
---------------------------------------------------------------------------------------------
сравним с исходным уравнением
неравенство превращается в равенство только в случае
=>
возводи в квадрат обе части
первый корень легко угадывается
не принадлежит промежутку (0; 3)
Ответ:
