Question

Найти углы прямоугольного треугольника, если его гипотенуза равна 4, а площадь равна 2



66 баллов​

Answer 1

Ответ:

$\frac{\pi}{12} \: u \: \frac{5\pi}{12}$

или

15° и 75°

Объяснение:

Обозначим в прямоугольном треугольнике

катеты как a, b

гипотенузу как с (с = 4)

и углы как $\alpha \: u \: \beta$

Причем углы связаны формулой

$\alpha \: = \: 90^o - \beta < = > \alpha \: = \: \frac{\pi}{2} - \beta$

Тогда площадь треугольника, равная 2, равна половине произведения катетов:

$S = \frac{1}{2} \cdot{a}\cdot{b} = 2$

Однако для острого угла в прямоугольном треугольнике отношение прилежащего катета к гипотенузе - это косинус угла, а отношение противолежащего катета к гипотенузе - это синус угла

Соответственно, каждый из катетов можно выразить через синус и косинус одного из острых углов:

$\cos\alpha = \frac{a}{c} = > a = c \cdot \cos \alpha \\ \sin\alpha = \frac{b}{c} = > b = c \cdot \sin \alpha$

Т.к. с = 4, получаем:

$a = 4 \cos \alpha \\ b = 4 \sin \alpha \\S = \frac{1}{2} \cdot{a}\cdot{b} = 2 \\ \frac{1}{2} \cdot 4\sin\alpha\cdot{4cos\alpha}=2$

Получаем ригонометрическое уравнение:

$\frac{1}{2} \cdot4\sin\alpha\cdot{4cos\alpha}=2 \\ 4\sin\alpha\cdot{4cos\alpha}=4 \\ 4\sin\alpha\cdot{cos\alpha}=1\\ 2\sin\alpha\cdot{cos\alpha}= \frac{1}{2 }\\ \sin 2\alpha = \frac{1}{2} \\ 2\alpha = ( - 1)^{k} \arcsin( \frac{1}{2} ) + \pi{k}, k \in Z$

$\arcsin( \tfrac{1}{2} ) = \frac{\pi}{6} ; \: \pi -\arcsin( \tfrac{1}{2} ) = \frac{5\pi}{6} \\ 2\alpha = ( - 1)^{k} \cdot\frac{\pi}{6} + \pi{k} =\bigg[ \large^{ \frac{ \pi}{6} + 2 \pi{n}, \: \: n \in Z } _{\frac{5\pi}{6} + 2\pi{m} , \: m \in Z} \\ \alpha = \bigg[\large^{ \frac{ \pi}{12} + \pi{n}, \: \: n \in Z } _{\frac{5\pi}{12} + \pi{m}, \: \: m \in Z } \:$

Т.к. мы ищем углы в прямоугольном треугольнике, то

$0 \leqslant \alpha \leqslant \frac{\pi}{2}$

Соответственно попадают в этот интервал только следующие полученные углы:

$0 \leqslant \frac{\pi}{12} + \pi{n} \leqslant \frac{\pi}{2} , \: \: n \in Z \\ 0 \leqslant \frac{1}{12} + {n} \leqslant \frac{1}{2} , \: \: n \in Z \\ - \frac{1}{12} \leqslant \frac{1}{12} + {n} - \frac{1}{12} \leqslant \frac{1}{2} - \frac{1}{12} , \: \: n \in Z \\ - \frac{1}{12} \leqslant {n} \leqslant \frac{5}{12} , \: \: n \in Z = > n = 0 \\ \alpha = \frac{ \pi }{12}$

$0 \leqslant \frac{5\pi}{12} + \pi{m} \leqslant \frac{\pi}{2} , \: \: m\in Z \\ 0 \leqslant \frac{5}{12} + {m} \leqslant \frac{1}{2} , \: \: m \in Z \\ - \frac{5}{12} \leqslant \frac{5}{12} + {m} - \frac{5}{12} \leqslant \frac{1}{2} - \frac{5}{12} , \: \: m\in Z \\ - \frac{5}{12} \leqslant {m} \leqslant \frac{1}{12} , \: \: m \in Z = > m= 0 \\ \alpha = \frac{ 5 \pi }{12}$

Итак, мы получили 2 пары углов:

$\small \alpha = \frac{\pi}{12} = > \beta {= } \frac{\pi}{2}{ - }\alpha = \frac{\pi}{2} {- }\frac{\pi}{12} = \frac{5\pi}{12} \\ \small \alpha = \frac{5\pi}{12} = > \beta {= } \frac{\pi}{2}{ - }\alpha = \frac{\pi}{2} {- }\frac{5\pi}{12} = \frac{\pi}{12}$

Очевидно, что это одна и та же пара углов, в зависимости от того, какой катет мы брали за а, а какой за b.

Итак, получаем Ответ:

Ответ:

$\frac{\pi}{12} \: u \: \frac{5\pi}{12}$

Answer 2

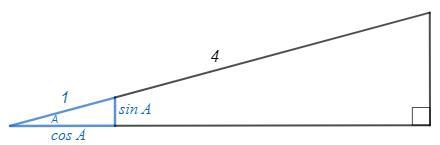
Рассмотрим треугольник, подобный данному с коэффициентом 1/4.

Его гипотенуза 1, площадь 1/8, катеты sinA и cosA.

S =1/2 sinA cosA =1/8 => 2 sinA cosA =1/2 =sin(2A) => 2A=30 => A=15°

B=90-15 =75°