Предмет: Математика,
автор: Риммулька
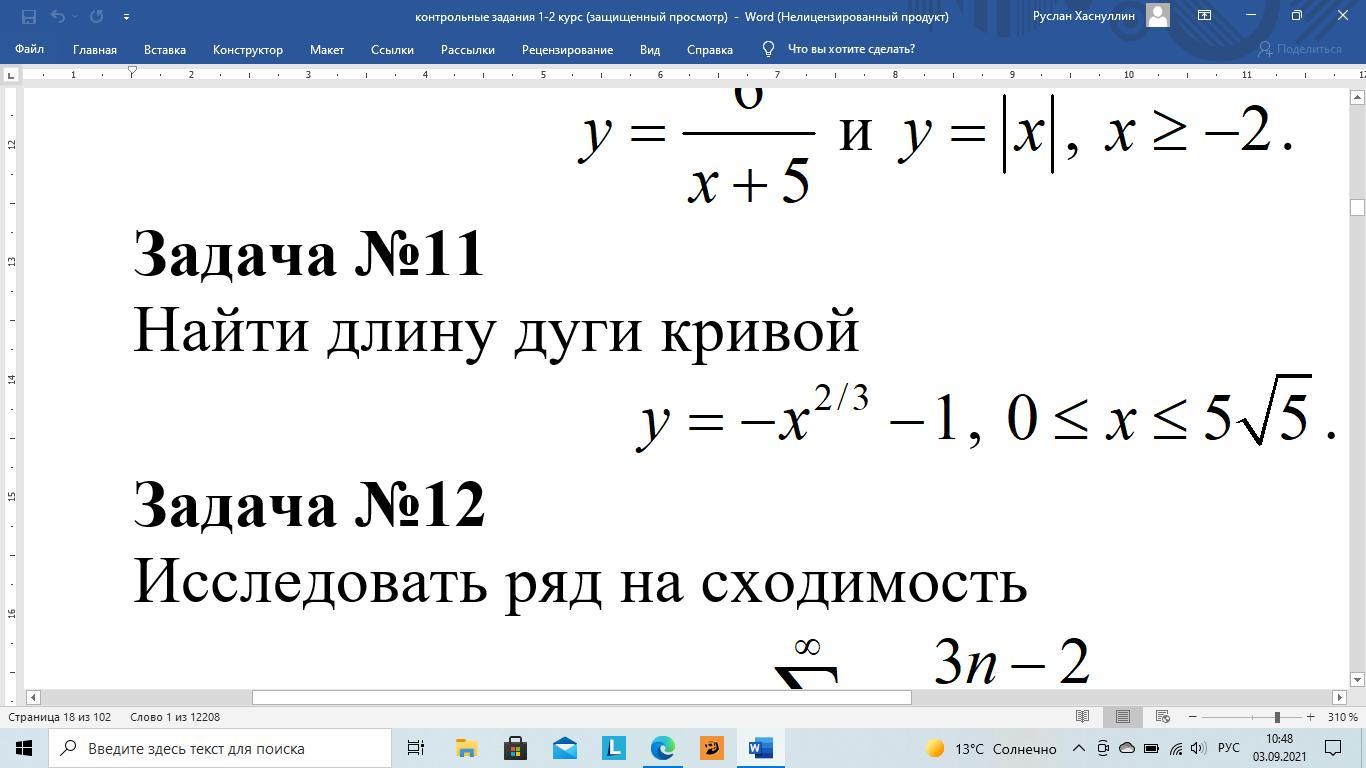
Помогите сделать 11 задание. Спасибо
Приложения:
Ответы
Автор ответа:
1
Ответ:
(он неберущийся, и задание было в другом)
Пошаговое объяснение:
Производная
Длина дуги =
anonimnyja142:
Здравствуйте, не могли бы вы, мне помочь. Пожалуйста
Похожие вопросы
Предмет: Английский язык,
автор: Cate1221
Предмет: Русский язык,
автор: vladimirisaev
Предмет: Русский язык,
автор: senyalugansk
Предмет: Химия,
автор: юлияя6