Предмет: Алгебра,
автор: king87544
решите пожалуйста даю 5 звезд
Приложения:
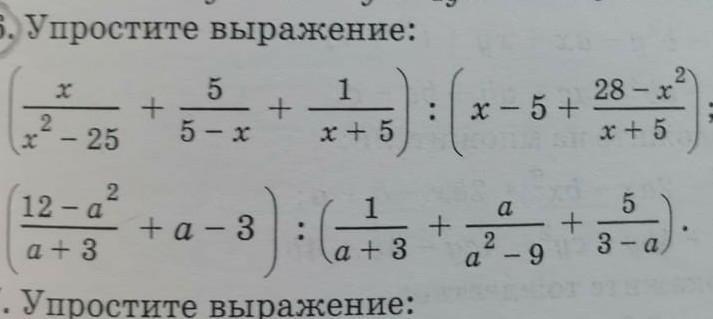
Ответы
Автор ответа:
1
Ответ:
Объяснение:
_________________________________________________________
Похожие вопросы
Предмет: Другие предметы,
автор: Fallout3and4
Предмет: Английский язык,
автор: пушистик9
Предмет: Русский язык,
автор: 89091582433
Предмет: Алгебра,
автор: pernik20121