Предмет: Алгебра,
автор: blindeye21
найдите корни уравнения
(желательно с расписанными действиями)
(за ответ не по теме - жалоба)
Приложения:
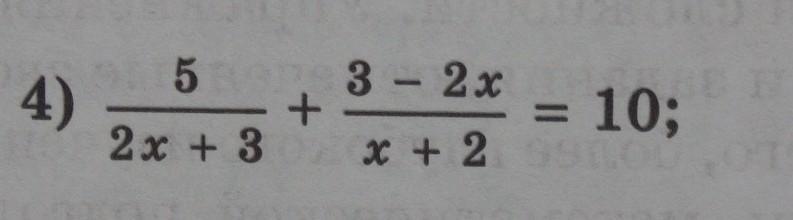
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Переносим все в левую часть, затем приводим к одному знаменателю
Раскрываем скобки:
Преобразовываем, сокращаем:
Получившееся уравнение равносильно следующей системе уравнений:
Решаем 1-е уравнение системы:
Оба корня не обращают знаменатель в ноль, поэтому входят в ОДЗ
Ответ:
blindeye21:
Благодарю
Похожие вопросы
Предмет: Русский язык,
автор: БадаловаА
Предмет: Русский язык,
автор: darcuriczyna
Предмет: Другие предметы,
автор: coolemelyanowa
Предмет: Математика,
автор: Люсявая