Предмет: Алгебра, автор: MadReyDeDay

Найдите значение выражения:
!) arcsin(sin7) (ответ: 7-2pi)
2) arcsin(cos8) (ответ: 5pi/2-8)

Ответы

Автор ответа: amkovoj15

Ответ:

sin7=7-2pi

cos8=5pi/2-8

MadReyDeDay: как?

Автор ответа: tracv9175

Ответ:

1) arcsin(sin7)=7-2π;

2) arcsin(cos8)=(5π/2)-8.

Объяснение:

Приложения:

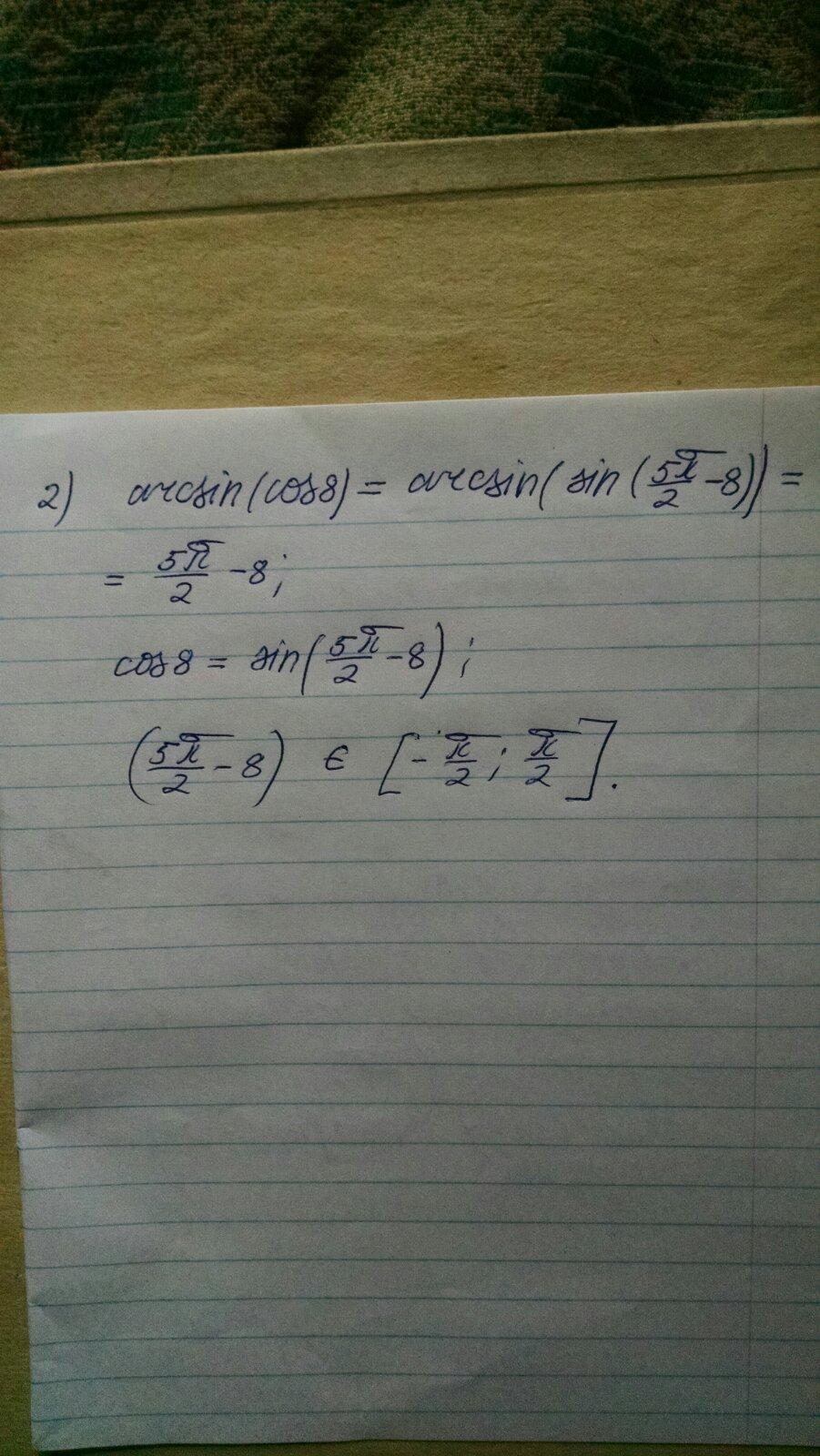
MadReyDeDay: как ты получил arcsin(SIN(5пи/2-8))?

tracv9175: arcsin(cos8): cos8=sin(5pi/2 -8), это формула аналогична формулам

tracv9175: cos(x)=sin(pi/2 -x); cos(x)=sin(3pi/2 -x); cos(x)=sin(5pi/2 -x)

MadReyDeDay: разве не cos(x)=-sin(3pi/2 -x)?

tracv9175: да это верно : cos(x)= -sin(3pi/2 -x). Рассматриваем ф-лы сos(x)=sin(5pi/2-x) которая аналогична ф-ле cos(x)=sin(pi/2 -x). Выбираем ф-лу cos(8)=sin(5pi/2 -8) потому что значение (5pi/2 -8) находится в пределах [-pi/2; pi/2]. Это область значений функции arcsin.

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Английский язык, автор: Kaban2001

5 вопросов про астану на английском языке 6 классу

1 год назад

Предмет: Другие предметы, автор: Akniet1111

найдите Что-то в слове "Сирень"

1 год назад

Предмет: Английский язык, автор: FEDYAU

КАК ПЕРЕНОСИТСЯ СЛОВО FRIDGE

1 год назад