Question

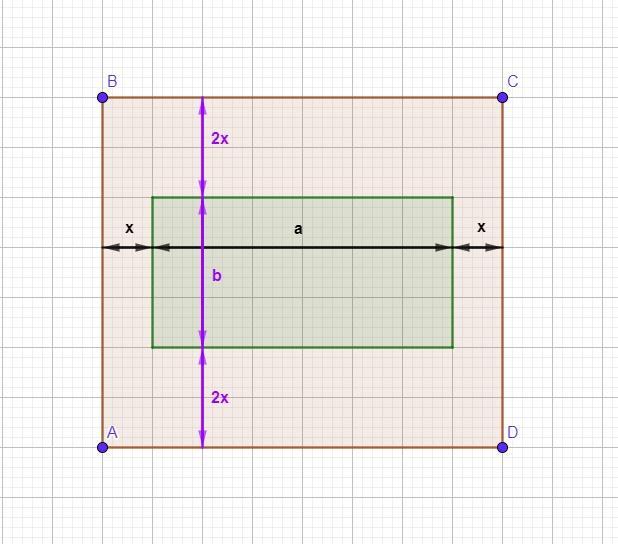
Прямоугольная фотография вставлена в деревянную рамку, ширина вертикальных частей которой в два раза меньше ширины горизонтальных. Периметр фотографии – 43 см, внешний периметр рамки – 73 см.
Чему равна ширина горизонтальных частей рамки? Ответ дайте в сантиметрах.

Answer 1

Ответ:

Ширина горизонтальных частей рамки равна 5 см

Пошаговое объяснение:

Прямоугольная фотография вставлена в деревянную рамку, ширина вертикальных частей которой в два раза меньше ширины горизонтальных. Периметр фотографии – 43 см, внешний периметр рамки – 73 см. Необходимо найти ширину горизонтальных частей рамки.

РЕШЕНИЕ

Фотография и рамка имеют форму прямоугольников.

Периметр прямоугольника можно найти по формуле:

Р=2(а+b),

где а и b соответственно длина и ширина прямоугольника.

1) Рассмотрим фотографию (зелёный прямоугольник).

Известно, что периметр фотографии равен 43 см. Примем длину и ширину фотографии соответственно за а и b. Тогда периметр фотографии будет равен:

2(а+b)=43, ⇒ а+b=21,5.  (1)

2) Рассмотрим деревянную рамку с внешним периметром ABCD (коричневый прямоугольник).

Пусть ширина её вертикальных частей будет равна х см, тогда согласно условию, ширина горизонтальных частей равна 2х см.

Тогда:

ВС=х+а+х= 2x+a,         (2)

АВ=2х+b+2x= 4x+b.   (3)

Внешний периметр рамки будет равен:

Р=2(АВ+ВС), по условию Р= 73 см, тогда:

73=2(АВ+ВС), => AB+BC=36,5.

Подставим значения АВ (2) и ВС (2) в данное выражение:

(4х+b)+(2x+a)=36,5

4х+2х+b+a=36,5

6x+(a+b)=36,5, так как  а+b=21,5.  (1), получаем:

6x+21,5=36,5

6x=36,5-21,5

6х=15

x=2,5

Таким образом ширина вертикальных частей рамки равна 2,5 см, а горизонтальных 2х=2×2,5= 5 см

ОТВЕТ: ширина горизонтальных частей рамки равна 5 см

#SPJ3