Question

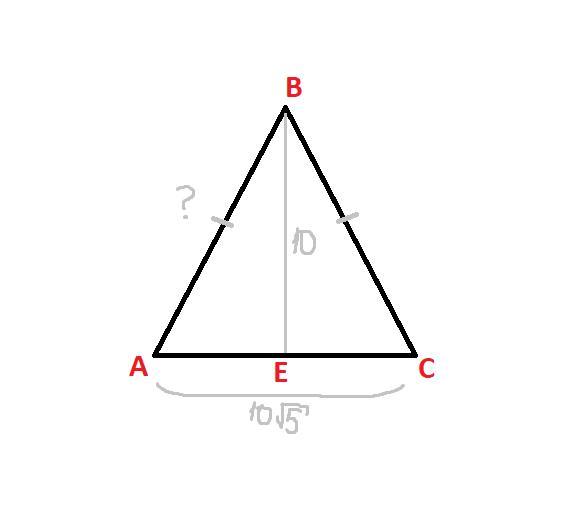
В равнобедренном треугольнике АBC , B E - высота, АB=BC . Найдите АB , если АC=10 √ 5 и BE=10​

Answer 1

Ответ:

AB = 15

Объяснение:

Равнобедренный треугольник -  треугольник у которого две равные боковые стороны (AB = BC - ?) и основание (AC = 10√5). BE = 10 - высота.

Рассмотрим прямоугольный треугольник Δ ABE (Δ ABE = Δ BEC). Знаем катет BE = 10, второй катет AE (AE = EC) - половина стороны AC а именно: AE = $\frac{10\sqrt{5}}{2}=5\sqrt{5}$. По теореме Пифагора найдем гипотенузу с помощью катетов, где a, b - катеты, c - гипотенуза:

$c^2=a^2+b^2\\AB^2=BE^2+AE^2\\AB=\sqrt{BE^2+AE^2}=\sqrt{10^2+(5\sqrt{5})^2} =\sqrt{100+25*5} =\sqrt{100+125} =\sqrt{225} =15$

Answer 2

Ответ:

AB = 15

Объяснение:

ΔABC - равнобедренный

АВ = ВС - боковые стороны

АС = 10√5 - основание

ВЕ = 10 - высота, опущенная н основание

----------------------------

АВ - ?

---------------------------

По теореме Пифагора

AB² = BE² + (0.5AC)²

$AB =\sqrt{BE^2 + (0.5AC)^2} =\sqrt{10^2 + (0.5 \cdot 10\sqrt{5})^2} = \\ \\=\sqrt{100 + 125} = \sqrt{225}=15$