с решением и дано , пожалуйста

Ответы
Перпендикуляр и наклонная
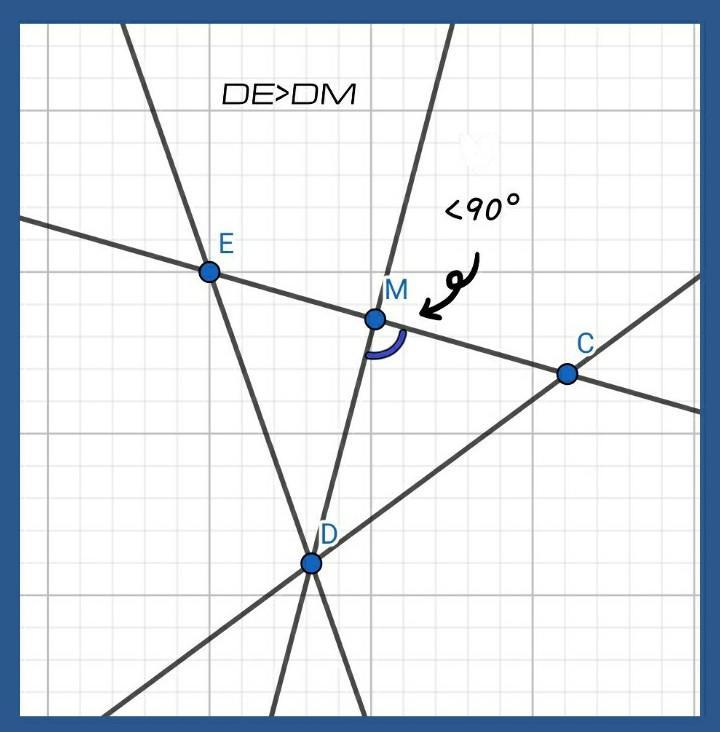
1) Из т.D опустим на прямую ЕС перпендикуляр. Прямой угол = 90°. Определим с какой стороны от т.Н (основание перпендикуляра) лежит т.М (если угол СМD<90°);
1.1) По теореме о сумме углов треугольника известно, что <МDC+<DCM+<CMD=180°;
1.2) Попробуем сдвинуть точку М по прямой ЕС вправо (так, чтобы т.М оказалась между точками Н и С); допустим, что ранее (по условию) угол CMD был n°; двигая т.М по прямой ЕС вправо, мы увидим, что угол МDC становится меньше (прямая DM будет «прижиматься» к прямой DC); угол МСD меняться не будет, тк ни луч СМ, ни луч CD не меняют своего своего положения; следовательно, если один из углов треугольника уменьшается (угол MDC), второй остаётся неизменным по градумной мере, то другой угол должен увеличиваться, чтобы правило о сумме углов треугольника (180°) сохранялось; Делаем вывод: при движении т.М вправо от т.Н угол СDM увеличивается; если угол СНD=90°, то при выше указанном положении т.М угол СМD будет > 90°, чего нам не нужно; значит, т.М должна расположиться слева от т.Н на прямой ЕС;
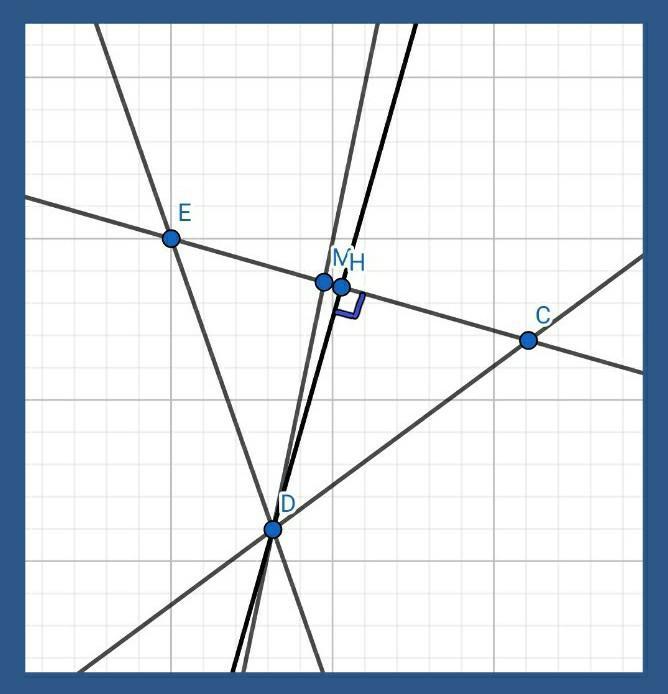
2) Далее воспользуемся теоремой о проекциях двух наклонных, опущенных к прямой из одной точки:
«У бо́льшей наклонной бо́льшая проекция»
Иными словами, чтобы узнать, какая из наклонных больше (DM или DE), нужно определить, проекция какой из двух наклонных больше) Если что, проекция наклонной - это отрезок, соединяющий основание перпендикуляра с основанием наклонной. В нашем случае проекция наклонной DM - это НМ, а проекция наклонной DE - это НЕ.
Далее легче.
3) По условию мы знаем, что т.М принадлежит отрезку ЕС; далее мы выяснили, что т.М и т.Е лежат по одну сторону от т.Н. Значит, исходя из базовых свойств отрезка (напишу их ниже), делаем вывод: НЕ=МЕ+НМ
Если отрезок НЕ - это сумма МЕ и МН (и МН≠0 по свойству отрезка), то НЕ>НМ. Т.е. проекция НЕ наклонной DE больше проекции НМ наклонной DM. Это значит, что наклонная DE>DM или DM<DE, ч.и.т.д.
Базовые свойства отрезка:
(которыми мы пользовались)
1) На прямой одна и только одна точка лежит между двумя другими;
2) Длина отрезка равна сумме длин его частей, на которые он разбивается любой его точкой;
3) Каждый отрезок имеет длину, большую нуля.
(p.s. надеюсь, всё понятно; конспектируйте уж сами))